APPH4010 Intro to Nuclear
Equations and Concepts for Intro to Nuclear
1. Basic Concepts
| Name of Concept/Equation | Definition/Equation | Notes | Example |
|---|---|---|---|
| Isotopes | same atomic number but different neutrons | ||
| Electron Volt | energy equal to the amount gained to accelerate rest electron through a potential difference of 1 volt | ||
| Atomic Mass Unit/Dalton | 1/12 of the mass of a neutral atom of $^{12}_6C$ | ||
| Magnetic Moment | Magnetic Dipole Moment associated with spin of nucleus | ||
| Spin Quantum Number | nucleons have spin of 1/2 in units of $h / (2\pi)$ | ||
| Mass to Energy | $E^2 = p^2c^2 + m_0^2 c^2$ | $m_0$ is rest mass, and if at rest, $p=0$ | $E_{\mathrm{electron}}=511keV$ |
| $E_{\mathrm{amu}}=931.5keV$ | |||
| Binding Energy | Energy required to separate its constituent nucleus | using $E=mc^2$ | |
| $B = [Z\cdot m_H + N\cdot m_N - m(A,Z)]c^2$ | energy used for binding, so the actual atomic mass $m(A,Z)$ is smaller | consider for carbon $^{12}_6C$ we have $m(A,Z)=12$, but $m_H=1.007825$ and $m_N=1.008665$ | |
| $m_H$ is mass of hydrogen so that it includes weight of electron | |||
| Binding Energy Curve | 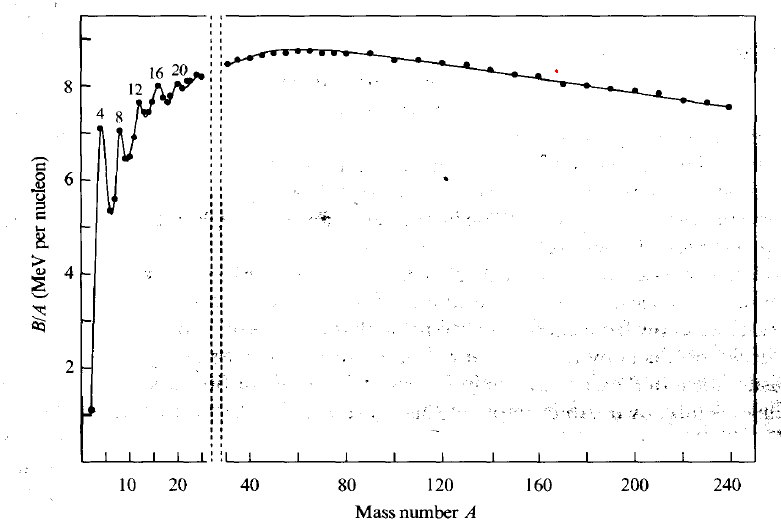 |
$B/A$ plotted because binding energy increases just as there are more proton to hold | |
| the more $A$, much much more $B$ is needed due to short range of internuclear force | |||
| but the above only works until a point where there is only a fixed number of neutrons affecting a proton | |||
| since higher $B$ also means more energy required to break = more energy released when making bonds, we want fission to go from right | |||
| Nuclide Stability Curve | 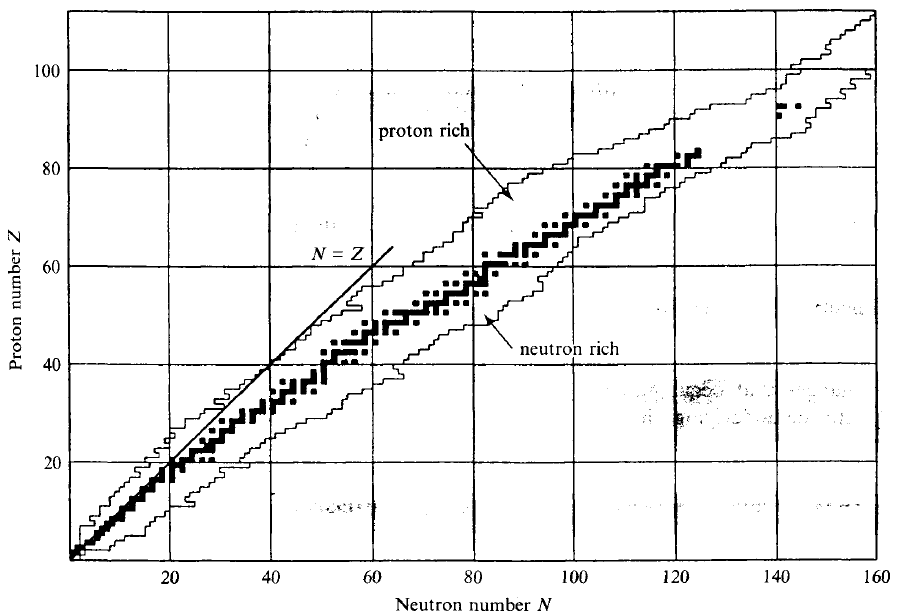 |
more neutrons is needed for more protons, hence this stability curve in the middle | |
| so above it is more proton then needed = proton rich | |||
| Properties of Radioactivity | Decay is a random process, but the probability of occurring can be modelled, and macro quantity such as $t_{1/2}$ can be computed | ||
| usually an unstable nuclide “parent” transforms into a more stable nuclide “daughter” | |||
| radioactivity measured in Becquerel = 1 decay per second | |||
| often heavy nuclei gives $\alpha$, and light nuclei $\beta$ | |||
| Alpha Emission Properties | $(A,Z) \to (A-4, Z-2)$ | preferred by heavy nuclides | |
| $\alpha$-particle is preferred because it is very stable, hence net effect of decay releases energy | (see below) | ||
| Decay Energy Released | $Q = \Delta m c^2 = (m_{\mathrm{left}}-m_{\mathrm{right}})c^2$ | if net mass loss = net energy released = RHS more stable = RHS less actual mass | U(238)$\to$ Th(234) + He(4) |
| $Q_\alpha = \mathrm{KE}{\mathrm{daughter}}+ \mathrm{KE}{\mathrm{\alpha}}$ | for alpha decay | ||
| $Q_\alpha = E_\alpha[1+ \frac{m_\alpha}{m_D}]$ | conservation of momentum | ||
| since $Q_\alpha,m_\alpha/m_D$ is known, this means KE energy spectrum for $\alpha$ will be discrete in this case | |||
| Beta Decay Properties | for proton-rich nuclides, often see $\beta^+$ decay or electron capture to convert $P \to N$ | $p \to n + e^+ + \nu$ | |
| $p+e^- \to n + \nu$ | |||
| otherwise, light nuclides often have $\beta^-$, which is $N\to P$ | $n \to p + e^- + \bar{\nu}$ | ||
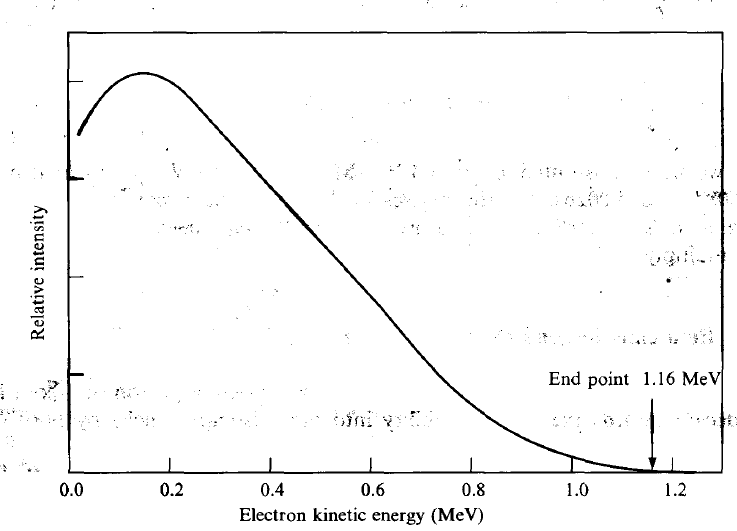 |
KE Spectrum of electron becomes continuous because you have three particles released | ||
| Gamma Decay Property | occurs when excited nucleus lose energy $\Delta E$ as photons | ||
| Rate of Radioactive Decay | $\frac{dN}{dt} = -\lambda N$ | Given that macroscopically the rate is proportional to number of radioactive nuclei | |
| $N(t)=N_0e^{-\lambda t}$ | $\lambda$ is probability per unit time that a nuclide decays | ||
| $A=\lambda N$ | since $\lambda$ is prob/time, activity is rate of decay of a sample, measured in Becquerel | ||
| Relativistic Effect | $\Delta T’ = \gamma \Delta T$ | high energy particle emitted so that $v \approx c$, then the actual half life becomes $\Delta T’$ | $v=0.995c$ when $\nu$ is released with large energy |
| $\gamma = \frac{1}{\sqrt{1-v^2/c^2}}$ | is Lorentz fraction |
5. Interaction of Radiation and Matter
Nuclear radiation normally consists of any particle with energy or photons (particle radiation is the radiation of energy by means of fast-moving subatomic particles). Its interactions with matter gives us opportunity for all experimental work. Therefore, this chapter we consider:
- how charged particle interact with matter
- how uncharged particle interact with matter
- how photons interact with matter
| Name of Concept/Equation | Definition/Equation | Notes | Example |
|---|---|---|---|
| Num Atoms and Atom Density | $N = \frac{m}{M}N_A$ | $m$ is mass of the substance you care, $M$ is the atomic weight of it | |
| $N/V = \frac{m}{V\cdot M}N_A = \frac{\rho}{M}N_A$ | $\rho$ is the density of the substance you are | $H_2O$ has $\rho \approx 1g/\mathrm{cm}^3$, and $M=18.0153$ | |
| Heavy Charged Particles Interaction Properties | Two Ways of Interaction: 1) its electric field can ionize atoms in its passage 2) collision (e.g. with electrons) |
||
| Deflect very little from path because its heavy | |||
| Well-defined range, depending on its energy, mass, charge, and the stopping medium | |||
| $\Delta E \approx E_\alpha(\frac{4m_e}{M_\alpha})$ | max energy lost per collision | incident alpha particle | |
| Though short range, as it can produce ionization = excited nuclei produces x-rays = need thicker $>R$ protection layer | |||
| Stopping Power | Rate at which a particle loses energy per unit path length | ||
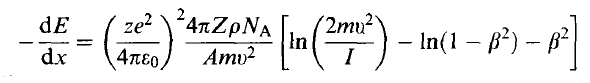 |
Bethe-Bloch Formula | ||
| Energy Dependence of Stopping Power | 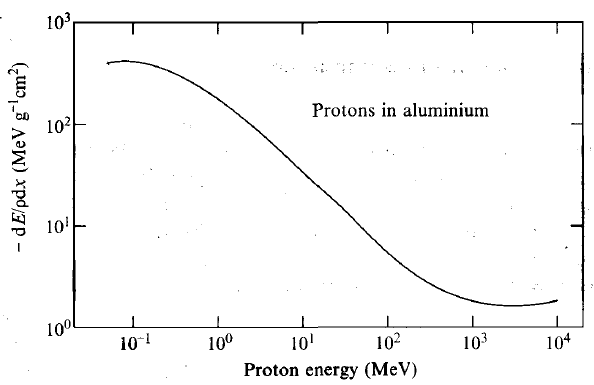 |
variation of stopping power with energy if incident proton. This general shape works for any charged ion | |
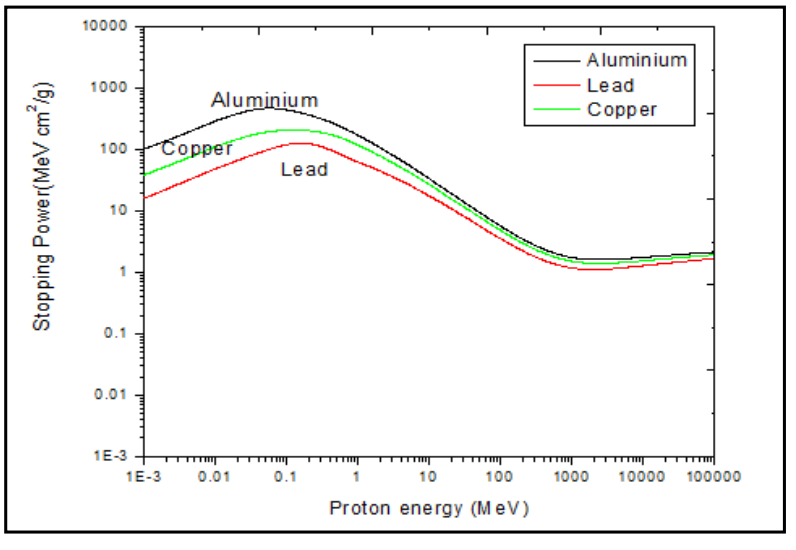 |
|||
| $\frac{dE}{dx} \approx \frac{\mathrm{const}}{E^k},k\approx 0.8$ | the faster the ion travels, the less chance it interacts with stopping medium, hence negative slope | ||
| $R=\int_{E}^0 dE/(dE/dx) \propto E^{k+1}$ | derived from above | ||
| Projectile Dependence of Stopping Power | $dE/dx \propto z^2 f(v)$ | depends on particle charge | |
| $R \propto (m/z^2) F(v)$ | range depends on incident particle mass and charge, derived from above | if two charged particle has the same energy, then $R_1/R_2 = (m_1/m_2)(z_2/z_1)^2$ because velocity is the same | |
| Stopping Medium Dependence of Stopping Power | $\frac{R_1}{R_2} \approx \frac{\rho_2 \sqrt{A_1}}{\rho_1 \sqrt{A_2}}$ | depends on stopping medium’s density and mass number | |
| Bragg Curve | 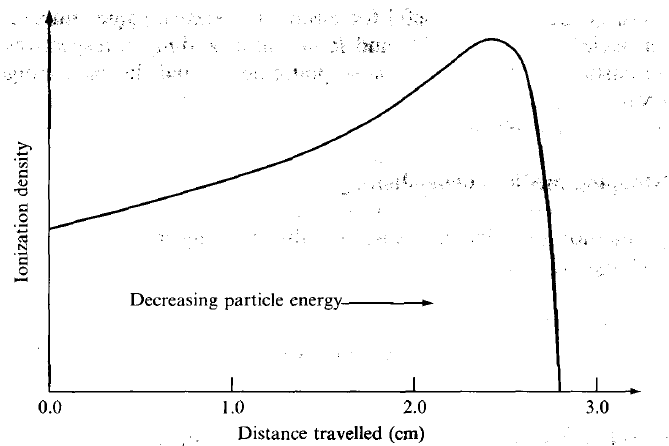 |
utilize the fact that stopping power increases when energy decreases | |
| particle travels slower = can produce more ions per unit path | |||
| hence Brag Peak = peak stopping power = peak ionization energy | hit tumor at this distance | ||
| when all energy is lost, it does nothing and stops/halts | |||
| Electrons/$\beta$-particle Properties | Two Ways of Interaction: 1) its electric field can ionize atoms in its passage 2) collision (e.g. with electrons) |
||
| a zig-zag path | |||
| a much faster speed = less stopping force | |||
| less well-defined range, hence uses mean-free-path | mean free path is the average distance over which a moving particle travels before substantially changing its direction or energy | ||
| you can also use max-range $R_{\max}$ as a measure, in which case$\rho R_{\max} \propto E_{\max}$ | |||
| Stopping Power v.s. Electron Energy | 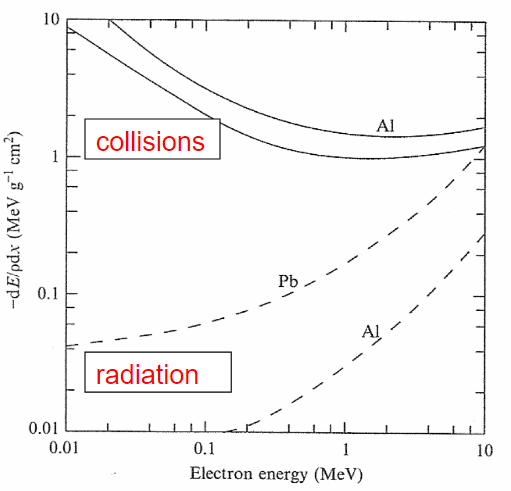 |
as electrons accelerate by rapidly changing directions, it emits a lot of Bremsstrahlung radiation meaning $-\frac{dE}{dx}_{\mathrm{rad}}$ contributes a lot to stopping power | |
| Reaction Cross Sections | measures area within which if you hit the particle near the target $T$, reaction will occur | can be used for both Neutron and Photon | |
| hence measures how strongly target $T$ reaction will occur | |||
| Microscopic Cross Section | $\sigma = \sigma(E)$ | $E$ is energy of incident particle | |
| unit is uslaly $\mathrm{cm}^2$ or in Barnes ($10^{-24}\mathrm{cm}^2$) | |||
| $\sigma_{\mathrm{total}} = \sigma_{\mathrm{abs}}+\sigma_{\mathrm{sca}}+\sigma_{\mathrm{n,2n}}+…$ | |||
| Reaction Rate | $R=N \cdot \sigma \phi = \Sigma \phi$ | $N$ is atomic density, $\phi$ is particle flux (particle per cm$^2$ per second) | |
| $\sigma \phi$ measures number of reactions triggered per second | |||
| Macroscopic Cross Section | $\Sigma \equiv N \sigma$ | is the macroscopic cross section | |
| Gamma Ray Interaction Properties | Primary ways of interaction: 1) photo-electric effect 2) Campton scattering 3) pair production |
because gamma rays are very energetic and they are photons | |
| we consider attenuation coefficient $\mu_m$ as a measure of probability the photon interact with material = photon vanished | |||
| Photoelectric Effect | photon absorbed by electrons (near nucleus for conservation of momentum) to be ejected | hence that photon disappeared = attenuated | |
| $T=E_\gamma - B_e = hv - B_e$ | $T$ is the emitted photoelectron and $B_e$ is the binding energy of the electron | ||
| secondary reactions might occur if 1) rest of the electrons rearrange themselves for de-excitation and release $\gamma$-ray 1) eject low energy electrons for de-excitation and hence Auger electrons to deal with the excess energy |
The Auger effect is a physical phenomenon in which the filling of an inner-shell vacancy of an atom, by an electron, is accompanied by the emission of another electron from the same atom instead of releasing energy. | ||
| $\sigma_{PE} \propto z^5 / E_\gamma^{3.5}$ | free electron = low probability of reaction | ||
| higher electron binding energy = more tightly bound electron has a higher chance (also for conservation of momentum) | |||
| Campton Scattering | 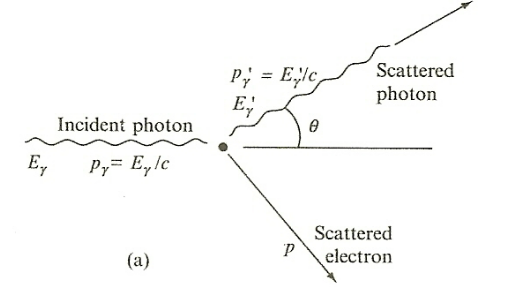 |
$\gamma$ ray scattered off electron and hence we get an electron recoiling and a lower energy photon | |
| $T = E_\gamma - E_{\gamma ‘} = E_{\text{KE of elec}}$ | |||
| $E_{\gamma ‘} = E_{\text{KE of elec}} = E_e - m_ec^2$ | for $E_e$ is the total energy of the recoil electron | ||
| $E_{\gamma ‘} = \frac{E_\gamma}{1+(E_\gamma/mc^2)(1-\cos \theta)}$ | energy of scattered photon from conservation of energy and momentum | ||
| a problem for shielding in real life as $\gamma$ photon didn’t disappear | |||
| Pair Production | creates an electron-positron pair (when heavy nucleus is near to conserve momentum) | ||
| $E_\gamma = 2m_ec^2 + T_- + T_+$ | $2m_ec^2$ is the rest mass energy of positron and electron | ||
| has secondary effect when positron recombine with electron $\to$ annihilate and produce two oppositely traveling photon $\to$ can do PE or scattering | |||
| Photon Attenuation | from the three mechanism above, photon either disappear or scattered = not observed by detector = attenuated | ||
 |
can measure and find out attenuation dependence on the three mechanism | ||
 |
difficult to measure | ||
| Collimated Photon Attenuation | $dI = - N\sigma I dx$ | $x$ is thickness of the material, $N$ is material atomic density, and $\sigma$ is interaction cross section | |
| $\mu \equiv N\sigma$ | linear attenuation coefficient | ||
| represents the probability per unit path length of a photon undergoing an interaction that would remove it from the beam | |||
| $I = I_0 e^{-N\sigma x} = I_0 e^{-\mu x}$ | intensity observed is $I$ | ||
| $\mu_m = \mu / \rho$ | mass attenuation coefficient | ||
| Photon Attenuation Coefficient Graph | 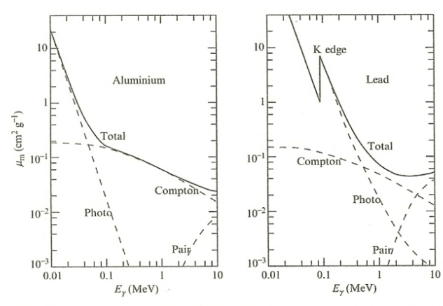 |
again, there are three phenomenon contributing to $\sigma$ hence $\mu_m$ | |
| Neutron Interactions | A variety of interactions but mostly nuclear reactions: 1) fission if neutrons at few MeV 2) scattering 3) slowed neutrons can give neutron absorption |
||
| Fission Fragments | When $N$ and $_{238}U$ react, it will create two fission fragment and 2-3 neutrons | hence neutron attenuated | |
| those neutrons can then start chain reactions | |||
| requires low neutron energy | |||
| Neutron Moderation | if elastic collision, can calculate energy $E$ of neutron with initial energy $E_0$ after colliding with some target nucleus at rest | ||
| $n = (1/\varepsilon) \ln(E_0 / E_n)$ | $n$ is the number of collisions of neutrons | ||
| $E_n$ is the energy of neutron after $n$ collisions | |||
| $\varepsilon = (2/A) - (4/(3A^2))$ | |||
| if reached low neutron energy = thermal neutron, can do fission | hence attenuated (see above) | ||
| Attenuation in Neutrons | $\sigma_T \approx \sigma_a + \sigma_s$ | mostly scattering and absorption | |
| $I = I_0 e^{-N \sigma_T x}$ | same equation as photon attenuation | ||
| $I = I_0 e^{-\Sigma x} = I_0 e^{- x/\lambda}$ | same $\Sigma = N\sigma_T$ as before | ||
| $\lambda = 1 / \Sigma$ | mean attenuation length = mean free path | ||
| $1/\lambda = (1/\lambda_a) + (1/\lambda_s)$ | since $\Sigma = \Sigma_a + \Sigma_s$ from the first equation |
6. Detectors and Instrumentation
Here, we consider the principle at systems for
- detection radiation
- producing controlled beams of radiation
In general, any detector gets its signal from the interaction of radiations with matter:
- collect charge released by ionization of gas (cased by radiation)
- excitation of electrons in semi-conductors (cased by radiation)
- observing fluorescent photons emitted due to de-excitation (cased by radiation)
- making ionization trails visible in film/solid gas (cased by radiation)
and in addition to detecting those radiations, we also want detectors to tell us more information such as energy of the radiation, type of the radiation, dose rate, etc.
-
dose rate is quantity of radiation absorbed or delivered per unit time
-
Dose equivalent (or effective dose) combines the amount of radiation absorbed and the medical effects of that type of radiation.
| Name of Concept/Equation | Definition/Equation | Notes | Example |
|---|---|---|---|
| Observe Current by Collecting Charge | $Q = \int_{0}^t i(t)dt$ | typically, radiation interact with matter and produces an electric charge (and ion) | |
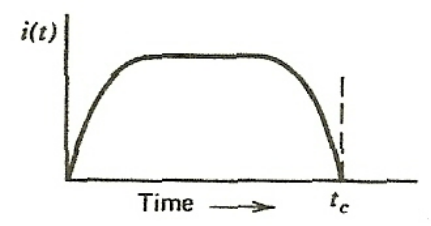 |
can collect that charge using an electric field = observe a current | ||
| notice the pulse like shape | |||
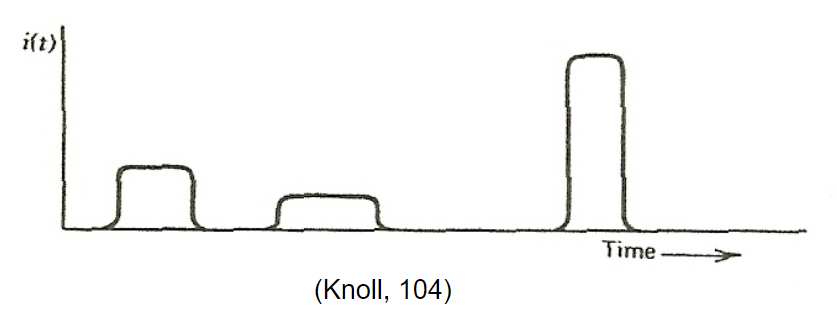 |
In reality, since radiation is random, it is better described by Poisson statistics | ||
| Poisson statistics = probability of a given number of events occurring in a fixed interval of time if the events occur with a known average rate and independently of the time since the last event | |||
| Modes of Detector Operation | Pulse mode: when low radiation flux hence each radiation can be recorded as separate pulse | ||
| Current mode: high particle flux hence average current is recorded | |||
| Detectors Figures of Metric | Things to check for a detector: 1) Energy Resolution 2) Detection Efficiency 3) Dead Time |
||
| Energy Resolution | 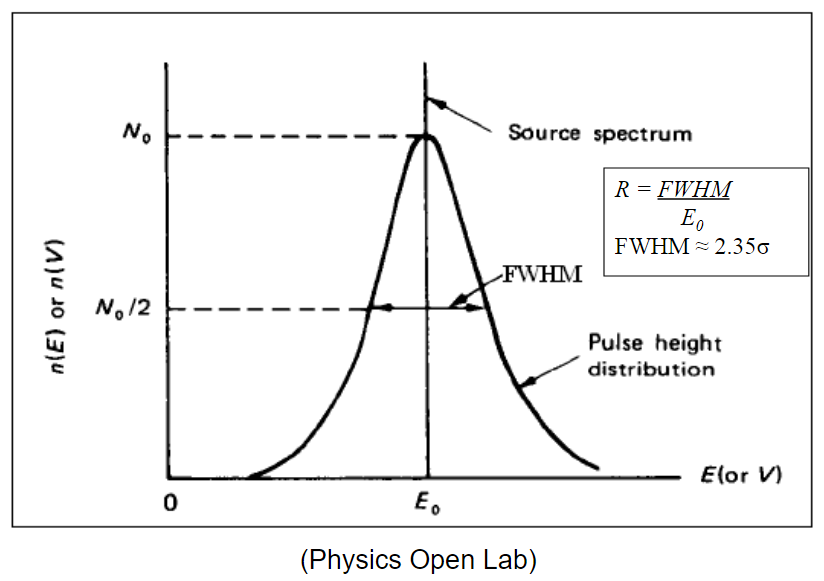 |
$E_0$ peak is the source, the Gaussian curve is the fitted energy spectrum measured | |
| measures Full-Width at Half Maximum (FWHM) | 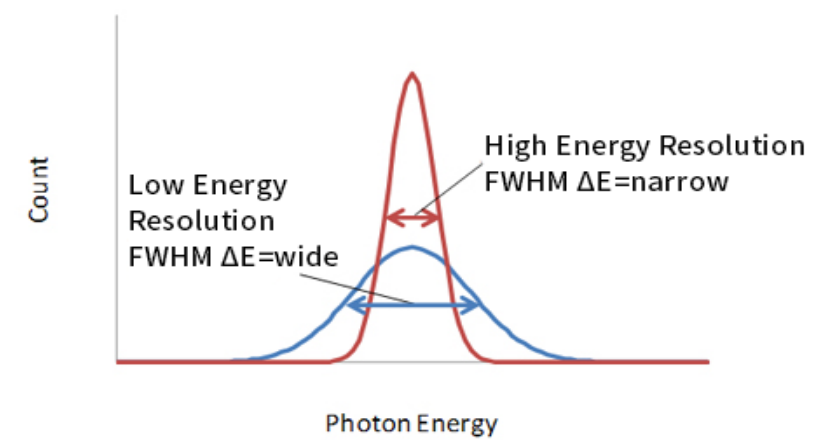 |
||
| measured in units of energy or percent of its peak energy $E_0$ | |||
| since it is usually first fitted to a Gaussian curve, then FWHM$=2.35\sigma$ | |||
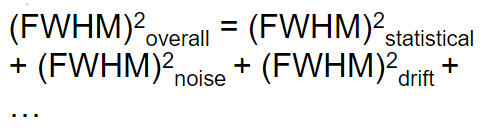 |
in reality due to all different effects reaching the device | ||
| Detection Efficiency | Measures how much radiation it can capture, and if captured, how much it can record | capture = radiation reaches it record = radiation reached AND recorded |
|
| usually easy to detect charged particles $\alpha$ and $\beta$, but be careful as they have short range | |||
| harder to deal with $\gamma, n$ because they have deposit little energy per unit path | |||
 |
depends on geometry of the device | if device is liquid so that source submerges in it, then it is $4\pi$ full coverage | |
 |
actual performance, dependent on detector material and thickness, and radiation type and energy | ||
| Dead Time | due to physical/electronical problem, there will be dead-time when device becomes unresponsive between events | e.g. takes time for the captured electron to travel to the cathode | |
| events almost overlap | |||
| $\tau$ = dead time | |||
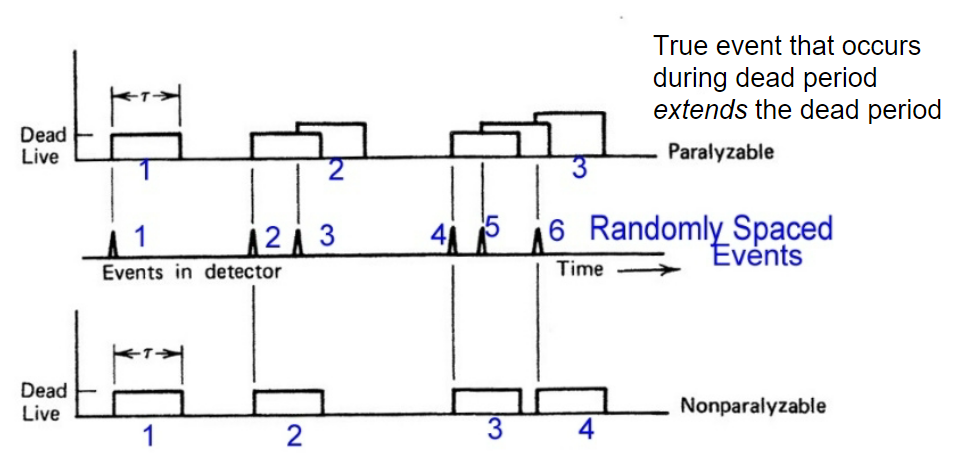 |
so non-paralyzable can recover 4 | ||
| paralyzable has the problem of extended dead time | |||
| Dead Time Corrections | Paralyzable detector: $n=me^{n\tau}$ | $n=$ true interaction rate, $m$ = recorded interaction rate, $\tau$ = deadtime | |
| Nonparalyzable detector: $n= m/(1-m\tau)$ | |||
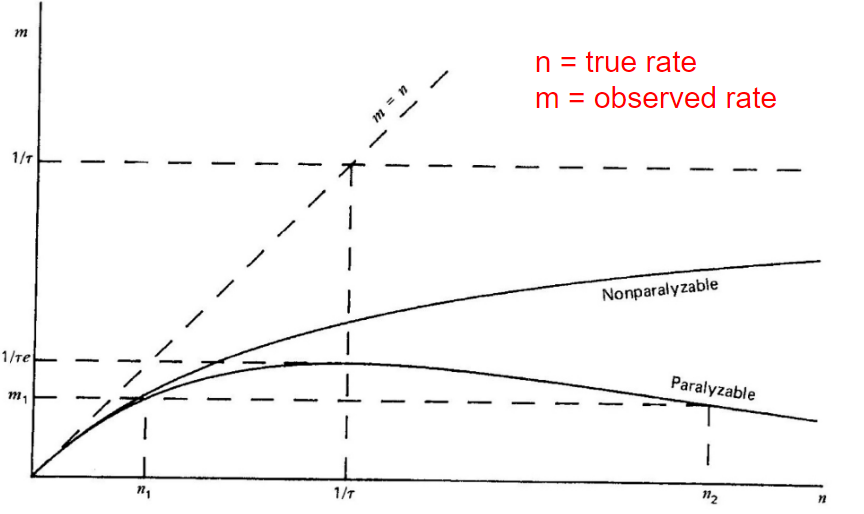 |
when true radiation $n$ is high, paralyzable can mistake it for a low $m$! | ||
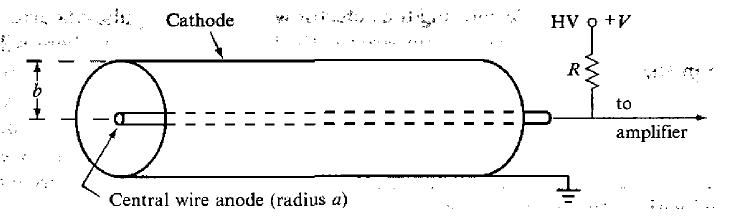
| Principles of Gas Detectors | detectors by using gas to be ionized by the radiation $\to$ record those ions | ||
| three types of detectors on this principle 1) ionization chamber 2) proportional counter? 3) GM counter |
|||
| Ionization Chamber | works by measuring ionization (of gas molecules) produced solely by incident ionizing particles (e.g. $\alpha$ radiation) | ||
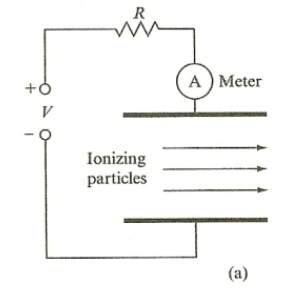 |
ionizing particles creates ionized gas $\to$ have a high enough field to prevent recombination $\to$ those ions complete the circuit by having electron goes to anode and positive ion to cathode | ||
| but usually needs an amplifier as current produced could be small | |||
| need a certain amount of electric field applied | see above | ||
| $A$ = #ions per sec produced $\times$ charge per ion | source disposing $1GeV\,s^{-1}$ energy per second and air in the chamber ionizes with $34$eV | ||
| #ions per sec produced = $10^9 / 34$ | |||
| Pulse Amplitude v.s. Voltage Applied in Gas Detector | 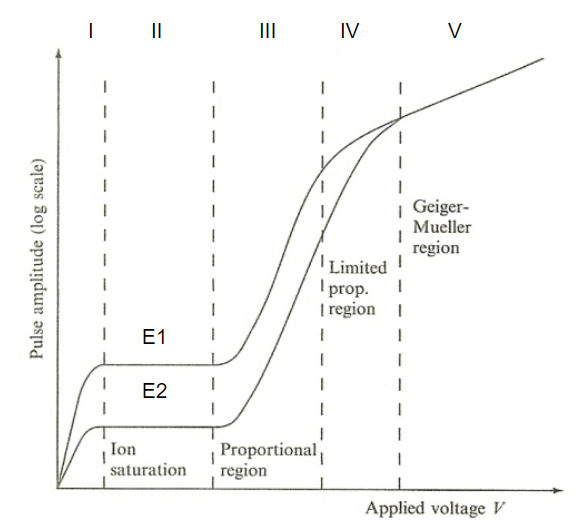 |
the fundamental reason why we have three types of gas detectors | |
| pulse amplitude can give you information of the energy of ionizing particles! | |||
| region I: increase $V$ means less recombination of ions | |||
| region II: full charge collection = no recombination | Ionization Chamber | ||
| region where output is independent of applied voltage | |||
| Gas Amplification Factor (GAF) = 1 | |||
| region III: electrons become more energized $\to$ can cause secondary ionization during collision. Those secondary ionized electrons can further produce ionizations | proportional chamber | ||
| amplification of current = Townsend Avalanche | |||
| GAF up to about $10^5$, but still proportional to the original ionization | |||
| region V: electrons so energized that it can excite inner electrons $\to$ UV radiation from de-excitation $\to$ ionizes other irrelevant atoms in the chamber | Geiger-Mueller Counter | ||
| can’t distinguish initial input energy of those ionizing particles | |||
| hence can only know the presence of those radiations | |||
| Proportional Chamber | electric field increased beyond region II, so that secondary ionizations occur | ||
| pulse amplitude still tells you energy of input ionizing particles | |||
 |
|||
| Geiger-Mueller Counter | electric field increased so much that everything is ionized = pulse amplitude does not depend on the energy of input ionizing particles | ||
| hence can only measure the presence of radiation | |||
| Scintillation Detector Mechanics | energy of radiation $\to$ excitation of electrons of scintillation material $\to$ de-excitation/Compton scattering which emits UV/visible light | ||
| those light photons are directed to the photosensitive surface $\to$ emit photo-electrons $\to$ amplified in PMT $\to$ observe pulse of current | |||
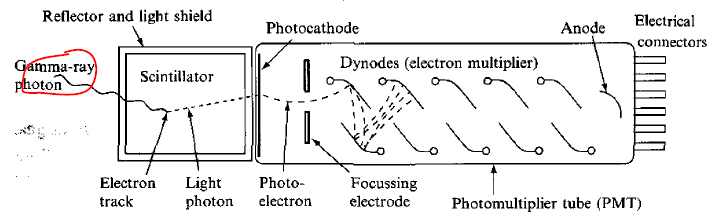 |
|||
| Scintillation Materials | need high effiiency of converting energy to photons | ||
| linear conversion: output proportional to deposited energy from radiation | |||
| short decay time = quick flash = short dead time | |||
| maximize conversion to output fluorescence | |||
| transparent to its own emission (which is photon, which is also energy) | |||
| Scintillation Types | Fluorescence=emit visible radiation with emission time approx. 10 ns | preferred | |
| Delayed fluorescence=above but loner emission time | |||
| Photofluorescence=longer wavelength and longer emission time | |||
| Semi-Conductor Detector Mechanics | energy of radiation creates electron-hole pair $\to$ electron move in the direction of applied field $\to$ current | works only if those e-h pairs do not recombine or get trapped in regions of impurity | |
| Semi-Conductor Detector Properties | only requires 3-4 $eV$ to create e-h pair, whereas to create ion pair in gas requires 30 $eV$ | ||
| better energy resolution | |||
| faster charge collection = shorter dead time | |||
| Semi-Conductor Detector Types | diode | ||
| high purity $Ge$ | see above | ||
| lithium drifted $Si$ or $Ge$ | alternatives to high purity, use $Li$ for drifting as dopant atoms | ||
| Thermoluminscent Detector | operates by accumulating radiation energy and read altogether at the end | ||
| therefore, we want crystals to de-excite as slow as possible when absorbed radiation | opposite of scintillation | ||
| mechanism: electron and holes are elevated but below conduction band, hence “trapped” | |||
| Neutron Detectors Properties | cannot detect neutrons directly, but secondary radiation, such as $(n,p)$ | ||
| depending on how fast the neutrons are, there are two types of neutron detectors | |||
| Slow Neutron Detectors Mechanism | for slow, thermal neutrons, nuclear reactions such as $(n,p),(n,\alpha), (n,f)$ have large cross section $\sigma \propto 1/v$ | basically can be triggered easily | $(n,p)$ means the reaction of $A+n \to B+p$ |
| mechanics: neutron $\to$ nuclear reactions $\to$ charged outputs (e.g. fission fragments) cause ionization $\to$ which can be measured | $^{10} B(n,\alpha)^7 Li$ | ||
| Slow Neutron Detector Types | Proportional Counter | $BF_3$ proportional counter performs $^{10} B(n,\alpha)^7 Li$ which a large cross section of 4010 b for thermal neutrons, and $Q=2.79MeV$ | |
| utilizes $(n,\alpha)$ | |||
| Fission Counters: coat detector with fissionable material | utilizes $(n,f)$ | ||
| Activation Counter: using activation foils composed of material sensitive of neutron of different energies | utilizes neutron capture | ||
| Fast Neutron Detector | use plastic or liquid organic scintillation material instead | $1/v$ means slow neutron detectors become not efficient | |
| in general, materials of rich hydrogen $\to$ recoiling protons produce energy for scintillation | |||
| Particle Identification | since radiation = any particle with energy, we might also want to know which particle it is | ||
| PI: Counter Telescope | stack two or more detectors, and can measure $\Delta E$ between detectors and $E$ total | ||
| $\Delta E$ can tell you stopping power | |||
| $E\times \Delta E \propto mz^2$ | |||
| PI: Time of Flight | measure time between detectors, hence determine $v$ | ||
| if radiation is pulsed beam, then you can just measure arrival time at detector and actual beam pulse | |||
| PI: Magnetic Analysis | use spectrometer with magnetic field to measure the deflection of charged particles | ||
| $r = mv/qB$, can measure mass to charge if known velocity | based on Lorentz Force $F=qv\times B$ |
Midterm Concepts
Chapter 1
- atomic structure
- plum pudding model, Rutherford model and its problems, Quantum Theory and its model, Bohr Model and its energy levels
- Rutherford scattering experiment, result
- equivalence of energy and momentum
- mass-energy equation
- uncertainty principle
- nuclear models
- liquid drop, shell model, their differences
- electron volt, alternative mass unit
- binding energy, mass excess, and Q calculation
- binding energy curve (reproduce)
- nuclear stability curve (reproduce)
- radioactivity equation and activity
- secular equilibrium
- alpha decay
- energy is discrete, etc
- beta decay
- continuous energy up to a cut-off
- auger electron
- number of atoms and atomic densities calculations
Chapter 5
- stopping power
- two components, use Bremsstrahlung
- Bethe-Bloch that
- stopping power goes $z^2 / v^2$
- stopping power v.s. energy curve
- bragg peak curve
- heavy charged particles
- how it loses energies, ionizing them and/or exciting them
- light charged particles
- zig zag, no well-defined range
- cross sections
- reaction rates, linear attenuation coefficient $\mu$
- attenuation and its differential equation
- photon ways of interacting
- three ways of how they work, but not formula
- neutrons interactions
- three ways, elastic, inelastic, or reaction
- thermal neutrons
Chapter 6
-
detector two operation mode
-
detectors figure of merit
- equation of FWHM/$E_0$
- efficiency, especially uncharged particles
- definitions of absolute/intrinsic effiency
-
dead time
- paralyzable v.s. non-paralyzable
- dead time correction equation
- dead time curves
-
will need to draw a detector
-
three types of ionization chambers
-
gas-field detector v.s voltage
- its five regions and the graph itself
-
scintillation detector mechanism
-
semi-conductor detector mechanism
-
TLDs
-
Neutron Detectoros
- slow.v.s fast needs hydrogen = moderates
- fission counter
-
particle identification
-
time-of-flight gives velocity + magnetic anlaysis
-
none of the detector mechanisms except in the particle identification to tell us particle type
-
Nuclear Structure
Aim:
- understanding what happens inside nucleus
- e.g. understand its properties by understanding what forces are responsible
- no complete theory today fully describes the structure and behavior of complex nuclei
| Name of Concept/Equation | Definition/Equation | Notes | Example |
|---|---|---|---|
| liquid drop model | nucleus regarded as a collection of neutrons and protons forming a droplet of incompressible fluid | ||
| good for systematic behaviors such as nucleon binding energy | |||
| discrepancies in liquid drop model = there is an ORDERED STRUCTURE within the nucleus in which neutrons and protons are arraged in stable quantum states in a potential well | |||
| Shell (Single-particle Model) | loosely held individual outer nucleons, which account for many of the nucleus’s properties | ||
| very alike the electron shell model and how electrons arrange themselves | |||
| Nuclear Force | binds nucleons in nucleus, n-n, p-p, p-n | extremely complicated, derivation from first principle | |
| Nuclear Force Properties | short range | ||
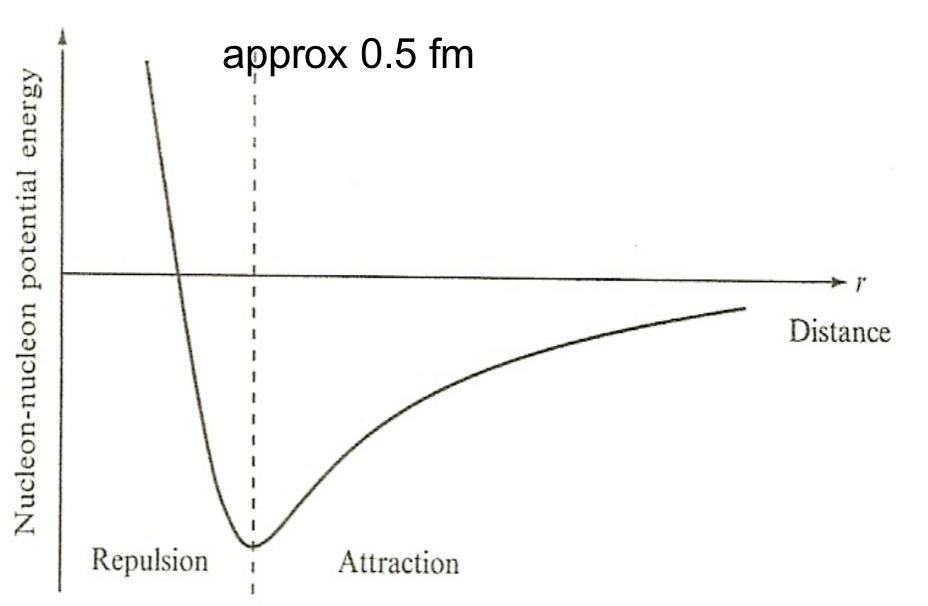 |
for very small separations, nucleons begin to repel = no clump | ||
| nuclear density approx constant for different sized nuclei = liquid drop | |||
| Nuclear Force Charge Dependency | charge symmetric: same nuclear force for p-p as for n-n | ||
| Nuclear Force Spin Dependency | Average force for p-n > p-p or n-n by a factor of about 2 | both n and p are fermions = obey Pauli Exclusion for spin | |
| so for p-p and n-n, you have to have different spin, net $S=0$ | |||
| n-p can have be either anti-parallel or paralell. Force in $S = 1$ state is stronger than force in $S = 0$ state. Therefore, avg. force for p-n is greater than that for p-p or n-n (by about factor of 2). | |||
| Explains why can have bound n-p (deuteron), but not bound n-n or p-p (i.e., nuclear force not strong enough to bind the latter two configurations) | p-p repulsion; n-n free particles + not strong enough force | ||
| Nuclear Force Spin-Orbit Coupling | $\text{Spin-orbit Force}=L \cdot S$ | $L,S$ being angular momentum and spin, respectively | |
| Force is attractive if S and L are parallel, and repulsive if they are anti-parallel | |||
| zero on average inside an atom | |||
| Semi-Empirical Mass Formula | 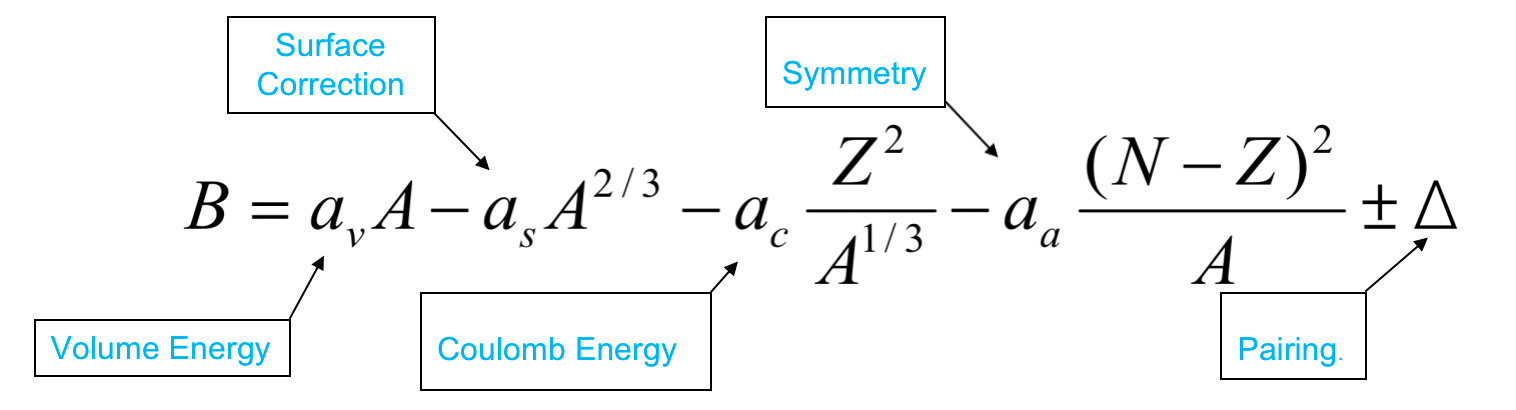 |
estimating binding energy, which can then be used to estimate the actual nuclear masses for unknown nuclei (but known $A$ and $N$) | |
| based on liquid-drop = estimates collective properties of a nucleus | |||
| SEMF Volume Energy | $a_vA$ term | nucleon feels the force only from its nearest neighbors and the nucleon density is approx constant = force is constant = B/A is approx constant in the interior of the nucleus. | |
| SEMF Surface Term | $A^{2/3}$ since the first $A\propto \mathrm{Volume}$ | reduced by a factor proportional to the surface area of the nucleus | |
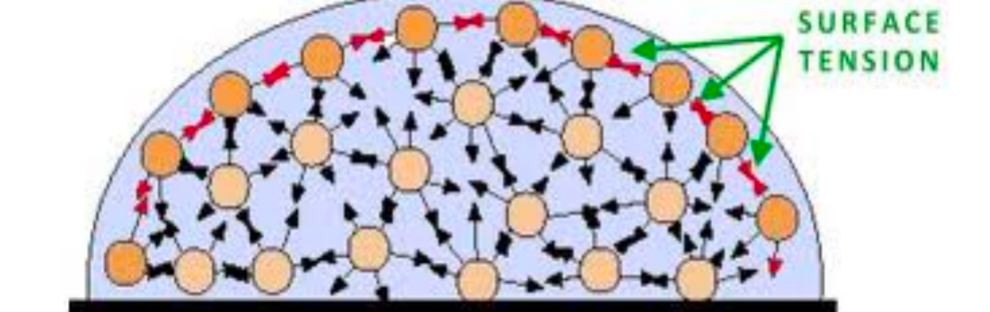 |
nucleons on the surface of the nucleus experience the nuclear force from nucleons inside the nucleus, but no force from the outside. hence reduced | ||
| SEMF Coulomb Term | $\propto {Z^2}/{A^{1/3}}$ | Coulomb repulsion would further reduce binding energy | |
| protons repel each other with a long-range Coulomb force; Mean radius of the nucleus is proportional to $R\propto A^{1/3}$ Coulomb force also $\propto Z^2$ |
|||
| SEMF Symmetry Term | $\propto (N-Z)^2$ | nucleus becomes more unstable the greater the difference between Z and N. Has the most effect for light nuclei | |
| shell model result. The term is zero for $Z = N$ and becomes less important for heavy nuclei (high A), where $N > Z$ | |||
| SEMF Pairing Term | $\Delta$ | nucleons tend to couple pairwise into more stable configurations | |
| Δ > 0 if N and Z are both even | from Pauli Exclusion Principle | ||
| Δ < 0 if N and Z are both odd | |||
| Δ = 0 if either N or Z is odd (i.e., A odd) | |||
| Nuclear Fission Energy Barrier | 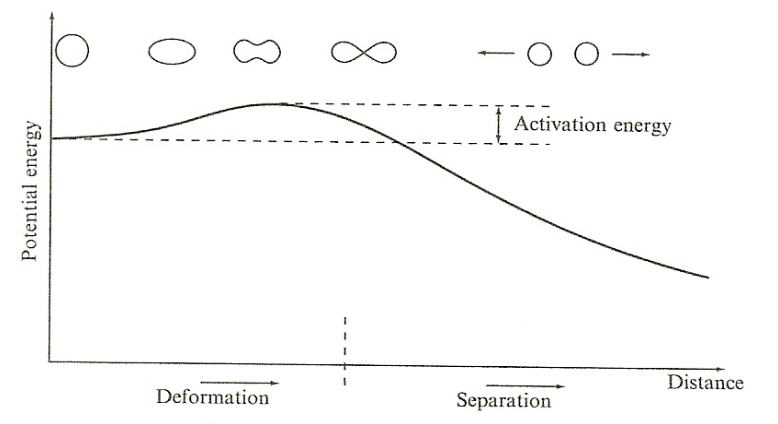 |
barrier to fission is called the fission barrier or activation energy | |
| for Heavy Nuclei | As s $A$ increases, the relative importance of the Coulomb repulsion term increases = it becomes energetically possible for the nucleus to split if it becomes deformed enough | ||
| Odd nuclei (($U_{92}^{235}$)) have very low activation energies, since the pairing term is zero, and can fission with low energy neutrons. | |||
| Isobaric Nuclei | same number of total nucleons but swapped #neutrons and #protons | will affect the coulomb term in SEMF | |
| Vibrational Model | 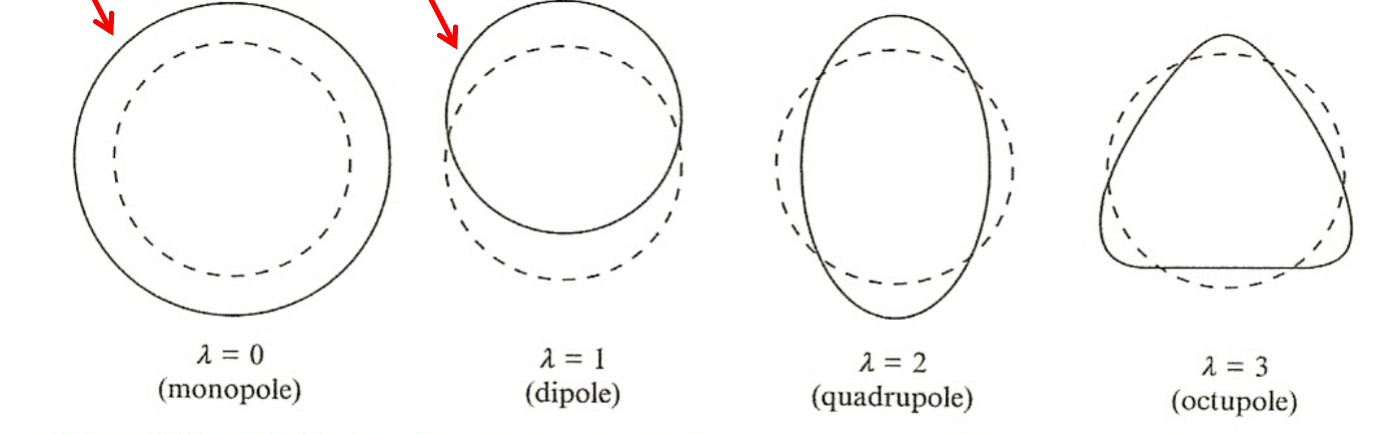 |
SEMF assumed sphere shape, but in reality can deform | |
| vibration can actually be modelled with liquid-drop model | |||
| Rotational States | rotation doesn’t produce any change of state | Collective rotational states can only occur in non-spherical nuclei (otherwise how do you know it is rotating?) | |
| Shell (Independent Particle) Model | aims to model energy level of nucleons | ||
| neutrons and protons fill energy level in the nucleus according to the Pauli Exclusion Principle | similar to electron energy levels | ||
| those structure like properties are not predicted by SEMF, which only deals with collective states | |||
| “islands of stability” corresponding to “closed shells,” also called “magic numbers,” | 2 (1s), 8 (2s, 1p), 20, 28, … | ||
| Nuclear Potential Energy | predict energy levels in the nucleus, need to know $V(r)$ | arises from interactions with other nucleons. | |
| infinite well = simplest model | |||
| Woods-Saxon Potential | $V(r) = -\frac{V_0}{1+e^{(r-R)/a}}$ | quite a good approximate | |
| Spin-Orbital Potential | 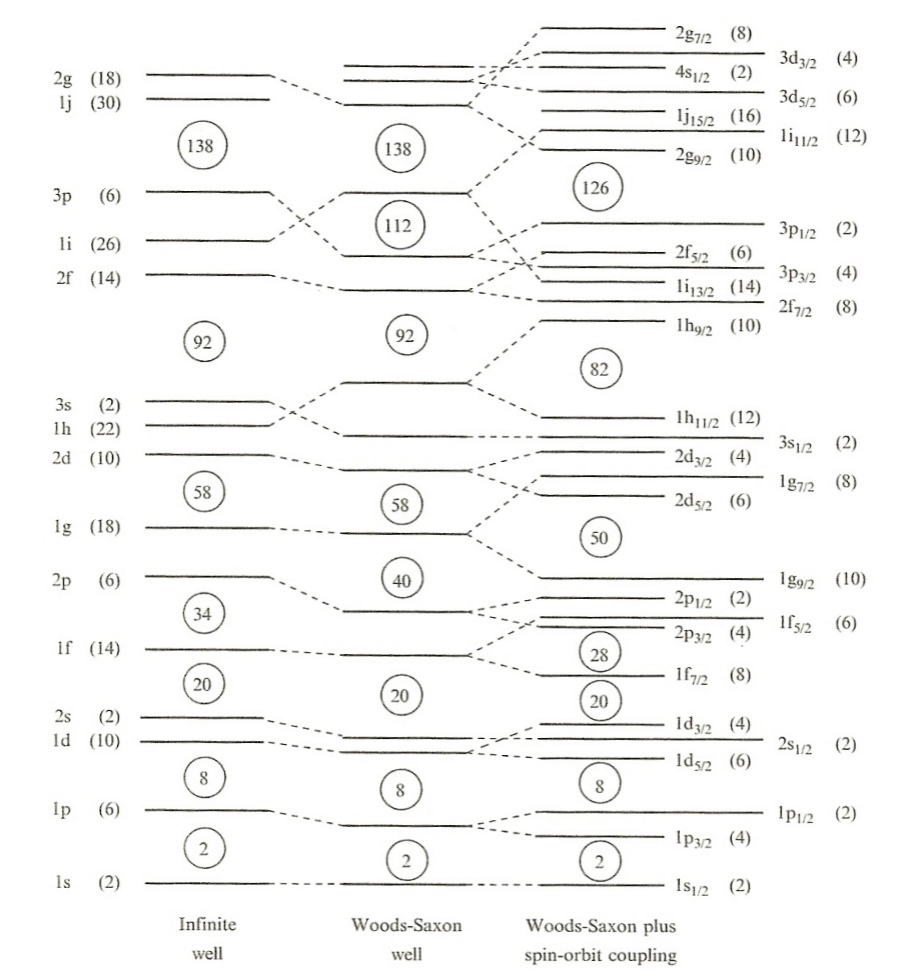 |
more complicated but accounted for more splittings of energy level | |
| splittings due to spin $s$ and angular momentum $l$. If aligned, $s\cdot l$ positive hence binding energy is increased |
Nuclear Instability
Aim: Predict/explain why
- some half-lives are short and others are long, and
- why certain energy transitions take place and others don’t
In general there will be a) electromagnetic force; b) weak force; c) strong force
| Name of Concept/Equation | Definition/Equation | Notes | Example |
|---|---|---|---|
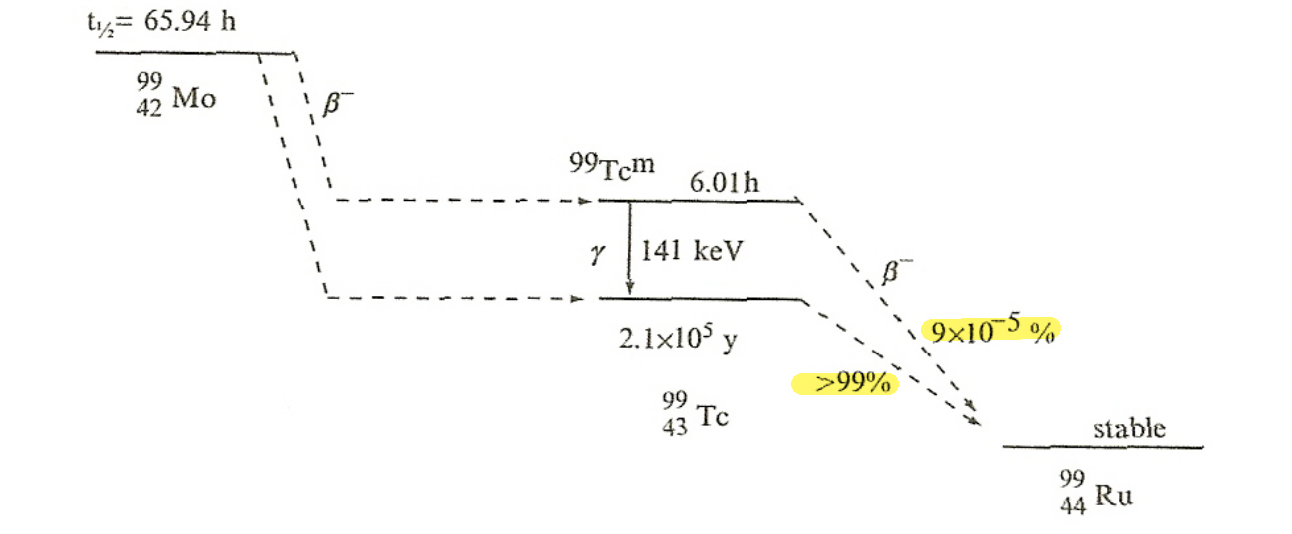
| Gamma Emission Mechanism | Excited nucleus may de-excite through $\gamma$-emission | help understand why certain gamma decay have longer half-lives than another | |
| gamma is “everywhere” in the sense that many radioactive decay accompanies gamma emission (see below, due to excited daughter nucleus) | |||
| Characteristic $\gamma$-emission | actually come from the transitions among the energy levels of the daughter nucleus. | 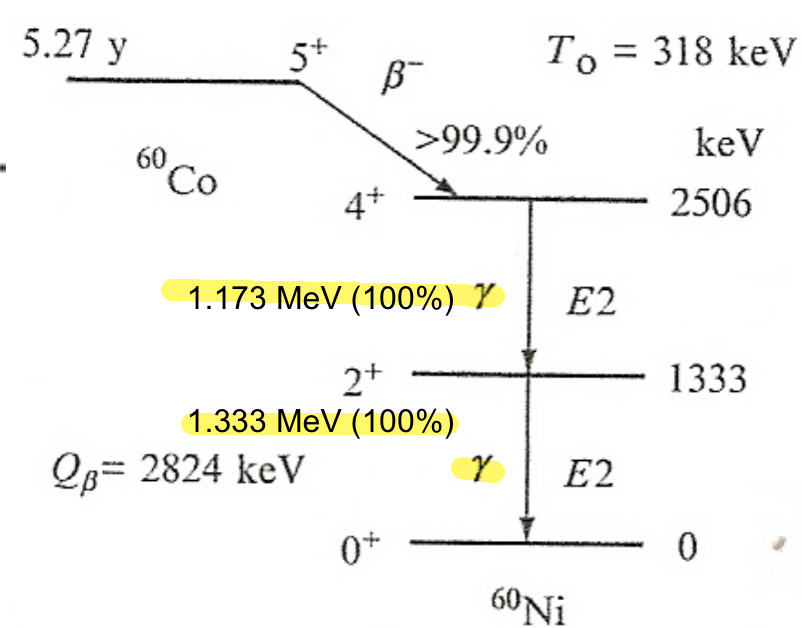 |
|
the above means we have two decays: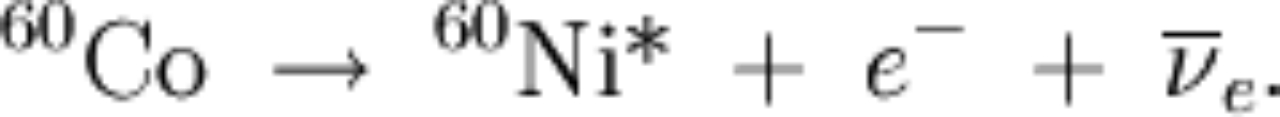 and then and then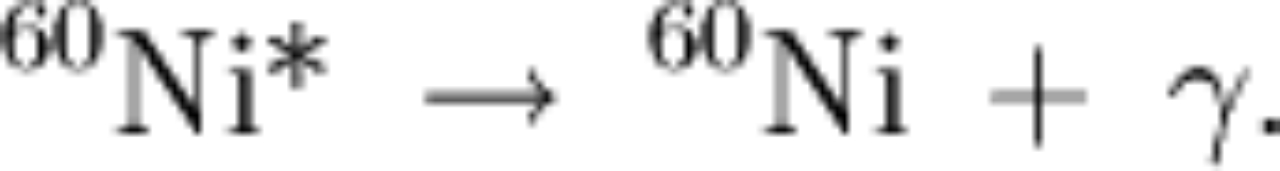 |
|||
| Selection rules | derived from consideration of conservation of angular momentum and parity, specify the allowable transitions among energy levels | answers: “why are some gamma more likely to happen than others?” | |
| 1. Photon that carries away energy has angular momentum $L>0$ | |||
| 2. Conservation of Angular Momentum: $\vert l_i - l_f\vert \le L \le \vert l_i + l_f\vert$ | $l_i$, $l_f$ is the angular momentum of the initial and final nuclear state | ||
| 3. Parity (wavefunction even or odd) is also conserved in EM transitions | whether or not a parity changed decides $\to$ | 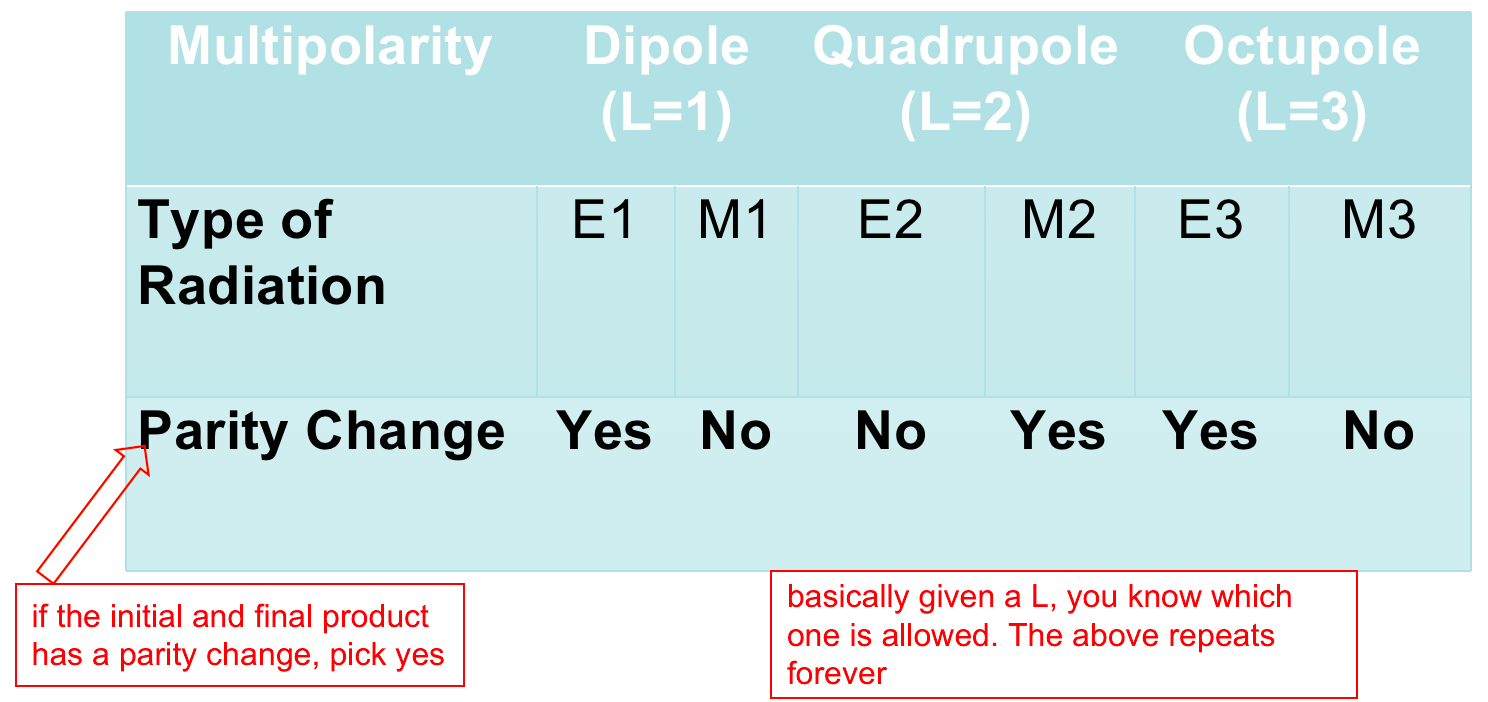 |
|
 |
|||
| do not provide information on the probability of its occurrence, only if it can occur | |||
| Competing Process in $\gamma$ | as gamma usually comes from de-excitaton, other processes such as de-excite with electron is competing (also comes from de-excitation) | ||
| e.g. Internal Conversion | transfer energy to an orbital electron (K-shell or further out), ejecting it from the nucleus | another way to de-excite = the parent and child would be the same as if performed gamma decay | |
| Single energy peak for each orbital electron transition unlike continuous β spectrum. | |||
| $\gamma$ Transition Rates | Weisskopf Single Particle γ Transition Rates | 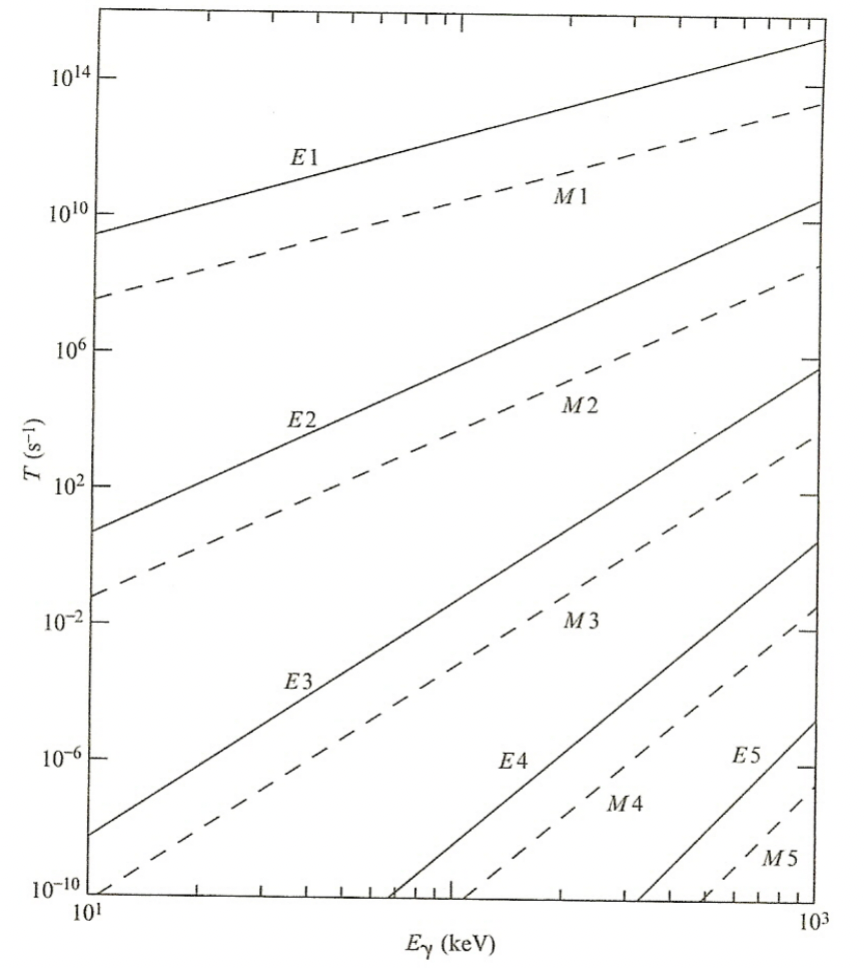 |
|
| $E_1$ is greatly favored | Selection rules allow E2, M3, E4, M5, and E6 transitions, but the E2 radiation is strongly favored. | ||
 |
|||
| If transitions have high multipolarity, T$_{1/2}$ may be considerable | basically for E6, M6, etc above, the probabiility is low = long half lives | ||
| Mixed $\gamma$ transitions | can substantially raise the probability that a particular energy γ-ray will be emitted | ||
| can’t characterize transition probability using the single particle model | |||
| Beta Decay Equations | 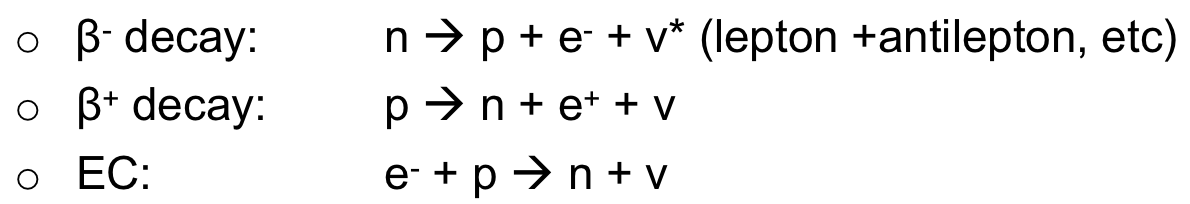 |
||
| allowed reactions = conservation of energy/momentum/charge/lepton number | |||
| can find the end point of the continous $\beta$ spectrum | recall that $Q$ gives the kinetic energy difference $Q = K_f - K_i = (m_i -m_f)c^2$ | $T_{end} = E_0 - m_e c^2$, the end point of the β spectrum. $E_0$ = total energy of the transition. | |
| Fermi’s Golden Rule | Probability of beta decay, determine the transition rate between an initial state (i) and a final state (f) for $\beta$ decay | ||
 |
$\lambda$ measures the transition probability | ||
| Electron Capture | competes with β+-decay when both modes are possible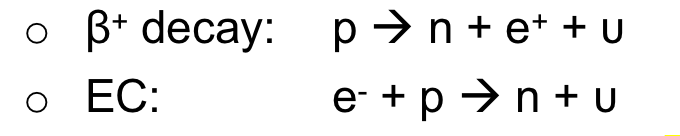 |
all $\beta$ are due to weak interaction | |
| Factor affecting EC probability/rate | depends on the overlap of the electron’s and the nucleus’s wave functions | ||
| 1. electron is most likely to be captured when it is closer to the nucleus | |||
| 2. higher Z = being attracted more = size of $K$-orbit electrons orbit is smaller = being captured | EC importance over β+ decay increases with Z | ||
| Alpha Decay | common decay mode for heavy radionuclides | ||
| Shed four units of mass (two neutrons and two protons) in one decay. | |||
| QM “tunneling” in Alpha Decay | heavy nucleus like uranium has barrier of 20MeV, but emitted alpha particle from it can be as low as 5 MeV. now we know it is due to non-zero wave function | ||
| requires $Q>0$ | |||
 |
explanation of QM tunneling | ||
| Preformation Probability | for alpha decay to happen, you need to first form the alpha particle in the nucleus | ||
 |
Nuclear Reactions
Study a bit further on how/when reaction happens
| Name of Concept/Equation | Definition/Equation | Notes | Example |
|---|---|---|---|
| Types/Classification of Reactions | Elastic scattering: a + A $\to$ a + A | scattering = Incident and outgoing particles are the same | |
| Inelastic scattering: a + A $\to$ a + $A^*$ | some energy goes into exciting internal levels in A, and later will go off $\gamma$ decay | ||
| Knockout: a particle is emitted (“knocked out”) from the nucleus | e.g. stripping of a proton from a carbon nucleus | ||
| Stripping reaction if the transfer is from the projectile to the target. | Transfer reaction: 1 or 2 nucleons are transferred between the projectile and target. | C-12 + alpha -> C-8* + alpha* | |
| Pickup reaction if the transfer is from the target to the projectile. | Transfer reaction, i.e. target nucleus gained | He-3 + p -> He-4* + gamma | |
| Direct nuclear reactions: formation of a “new” nucleus typically involve the transfer of just a few nucleons (protons or neutrons) between the colliding nuclei. | without the creation of an intermediate compound nucleus. | e.g. scattering | |
| Compound nuclear reactions: results in the formation of an intermediate compound nucleus, and can result in the emission of several particles | involve the transfer of many nucleons between the colliding nuclei | ||
| Resonance reaction: incoming particle has right energy to excite an energy level in the target nucleus, greatly increasing the cross section | |||
| Discern what Reaction happened with Energy Spectrum | can distinguish different mechanism because they give rise to outgoing particles have different energy | ||
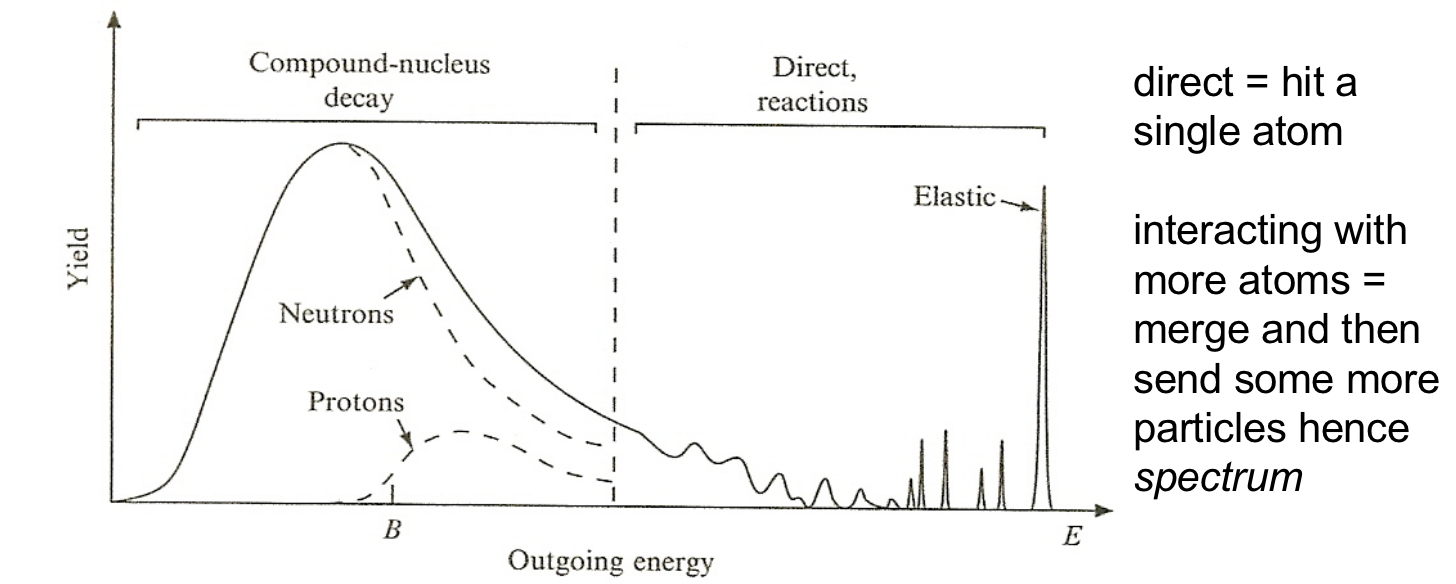 |
Discrete energy peaks at high energies from direct reactions | ||
| At lower energies, peaks correspond to more closely spaced energy levels can’t be resolved | |||
| At still lower energies, compound nuclei are formed, where neutrons and protons share the incoming particle energy and “evaporate” from the nucleus in a continuous spectrum | evaporate: formed compound nucleus $\to$ an equilibrium is reached so the compound nucleus loses its energy slowly over time by emitting particles, mostly protons and neutrons | ||
| Angular Distributions | angle of output particles relative to input particle | ||
| Angular Distributions for Direct Reactions | Direct collisions (few nucleons take part) usually produce forward peaked reaction products | forward peak = products traveling in the same direction as input | |
| Direct collisions = exhibit oscillations as a function of scattering angle due to the wave nature of the particles | |||
| Angular Distributions for Compound Reactions | Angular spectrum of evaporated particles from a compound nucleus is more isotropic | since the emitted particles “have no memory” of the direction of the incoming particle | |
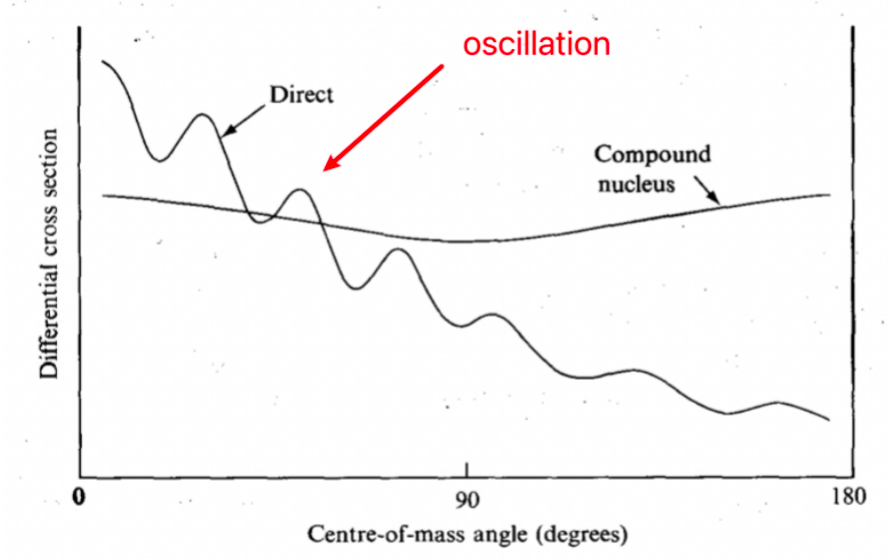 |
y-axis = prob of observing this | ||
| Reaction rate | each reaction has its own cross-section = own reaction rate | ||
| $R =\sigma N_A \phi=\Sigma \phi$ | σ = reaction cross section φ = particle (e.g., neutron) flux $N_A$ = the number of target atoms per unit volume |
||
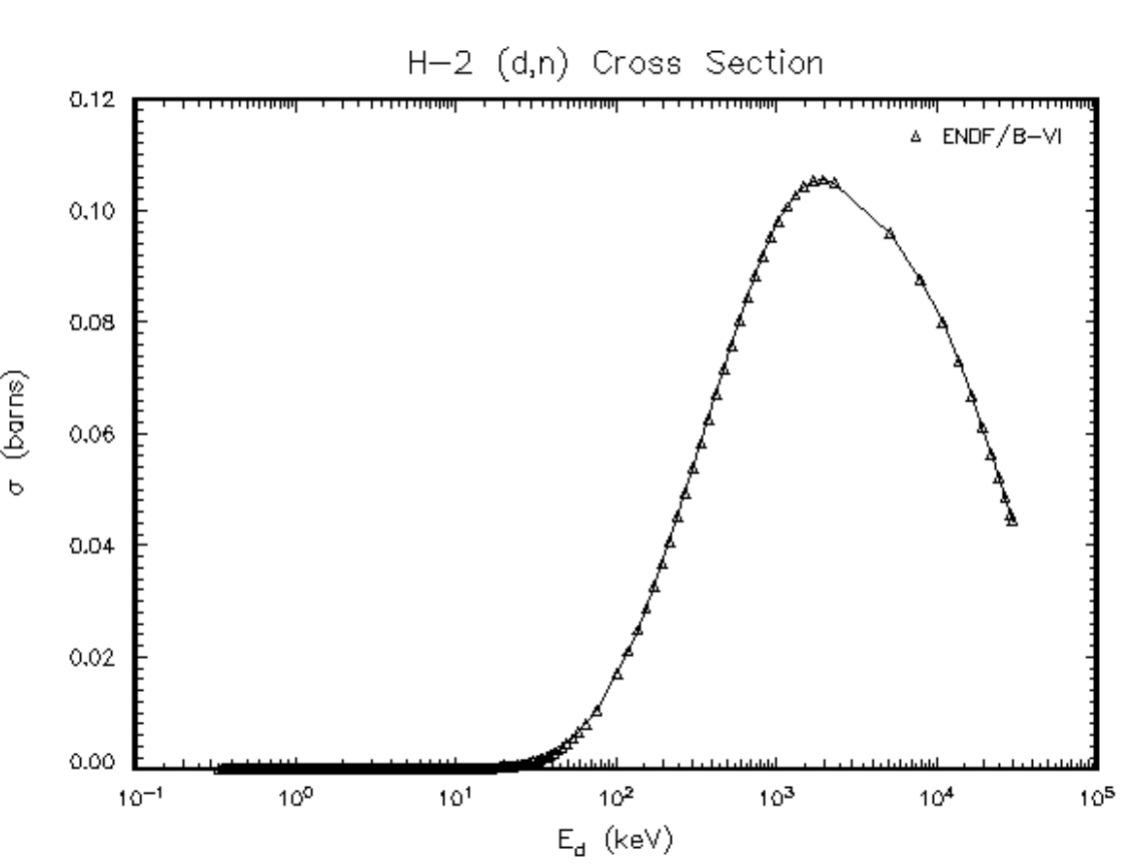 |
DD reaction cross section = higher E better because this is fusion | ||
| Classical Estimate of Reaction Cross Section Assumptions | calculate cross section itself (before we were given this) | ||
| assumptions = reaction happens when come close enough together for the strong nuclear force to act | |||
| Classical Estimate of Uncharged Particles | 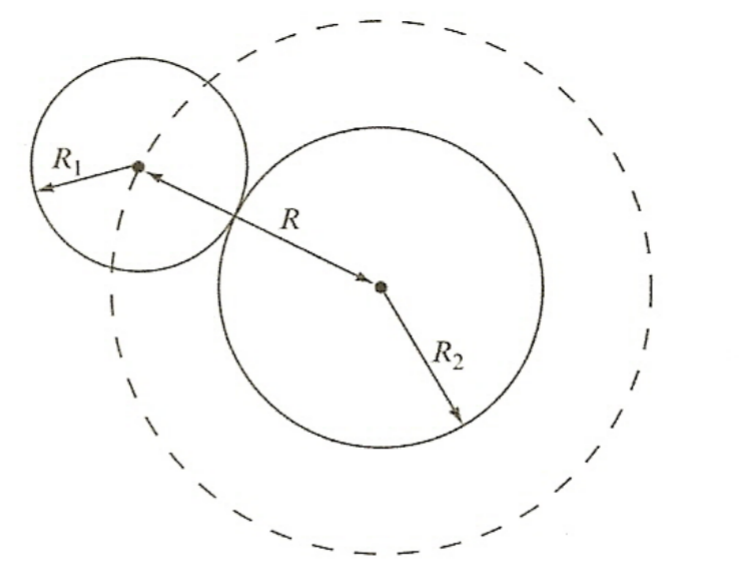 |
||
| $\sigma= \pi (R_1 + R_2)^2 = \pi R^2$ | |||
| Classical Estimates of Charged Particles | 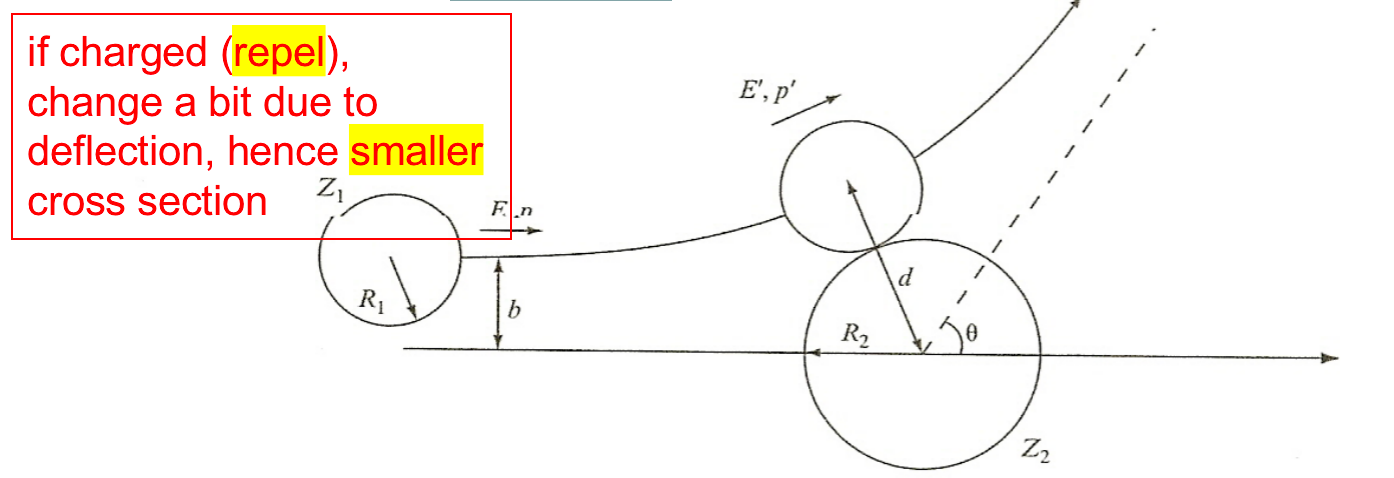 |
||
| Impact parameter, $b$ replaces $R$. $\sigma = \pi b^2 = \pi R^2 (1-B/E)$ |
means if $B>E$ reaction cannot occur | ||
| QM Estimate | classical works when particles is more ‘particle-like’ | classical approximation of reaction cross section is only decent for particles with de Broglie wavelength less than the size of the nucleus | |
| also kind of works if we are heavy ions = wavelength often smaller than nuclear dimensions | |||
| but if wave functions coincide, then reaction occur = can occur even if $B>E$ | in reality, high energy = looks like particle; low energy = looks like wave | ||
| Usage of Elastic Scattering for Nuclear Structure | force causing scattering depends on the spatial distribution of nucleus => by analyzing the way particles scatterd = know about the size and distribution of force field = know about the nucleus | ||
| Electrons make good probes of the nucleus since they are not absorbed and interact via the well-know electromagnetic force with the protons | if we take particles such as $\alpha$, then it interacts strongly once inside the nucleus = lose its identity and not reappear in the entrance channel | ||
| Compound Nuclear Reaction Mechanism | Many nuclear reactions proceed in two or more steps | ||
| 1. the incoming particle is absorbed by, and excites, the nucleus | |||
| 2. the nucleus loses its excitation energy (decays) through one of several different, possible exit channels (decay branches or decay channels) | |||
| Compound Nuclear Reaction Rate | Each decay channel is characterized by a probability and mean lifetime, $\lambda = 1/\tau$ | ||
| for compound reaction $A+a\to C\to B+b$ reaction rate is $\sigma_{\alpha, \beta} = \sigma_c (\Gamma_\beta / \Gamma)$ |
$\sigma_c$ is the cross section of forming the compound nucleus $\Gamma_\beta / \Gamma$ is fractional decay width into the final channel $B+b$ |
||
| basically, need $C$ to happen, and then also $\beta$ to happen | |||
| Energy width of Compound Nuclear Reaction | due to the Uncertainty Principle, uncertainties in $\lambda$ and $\tau$ $\to$ uncertainties in energies of the states $\to$ energy spread | ||
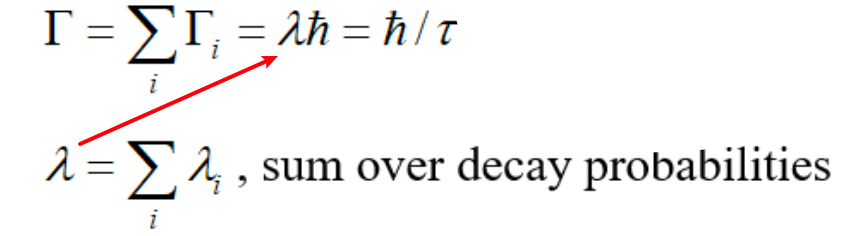 |
|||
| Cross Section Thresholds | 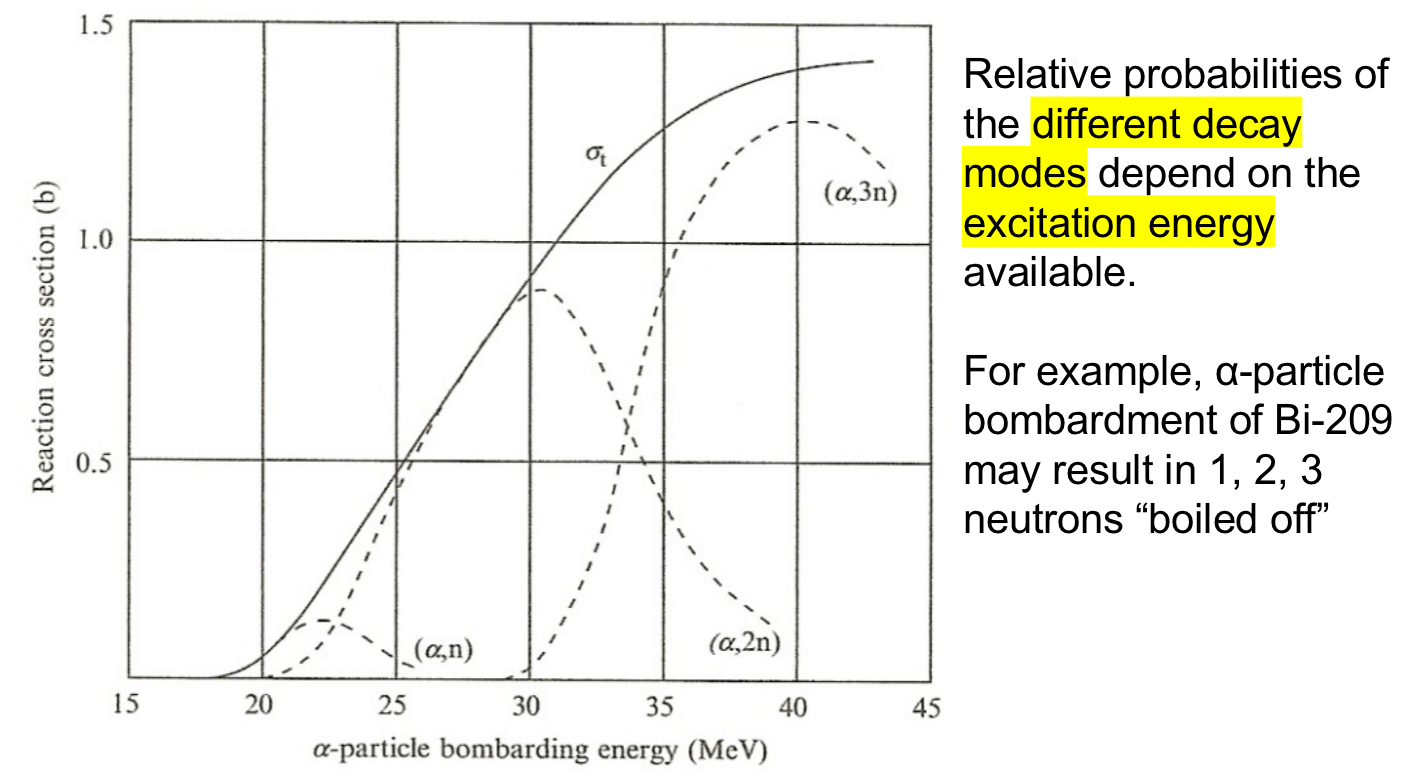 |
each decay mode also has its own ‘excitation energy’ required | |
| Heavy ion particle accelerator’s goal | Heavy ion particle accelerators are used to cause reactions where the target nuclei are blown apart or to attempt to create new heavy elements through absorption. |
Fission
This section will focus on induced fission from neutron absorption
- Some heavy “transuranic” (near uranium) nuclei can undergo induced fission if supplied with sufficient energy (7-8 MeV)
- about 6 MeV comes from binding of an extra neutron by the strong force and the rest from external sources
- an extra 1-2 MeV from pairing (depends on if your $N$ is odd or even)
| Name of Concept/Equation | Definition/Equation | Notes | Example |
|---|---|---|---|
| Why is Fission Energetic Useful? |  |
||
| Fissile nuclei can fission with low energy, “thermal,” neutrons | |||
| Energy during/Mechanism of Fission | 1. normally, the SEMF surface term provides a restoration force, like disturbing surface tension on water | ||
| 2. if sufficient energy is supplied, the shape will deform to such an extent that the Coulomb repulsion force will dominate = strong force only works locally = nucleus starts to break | |||
| 3. repulsive force will drive the (usually) 2 fission fragments apart and potential energy is converted into kinetic energy | |||
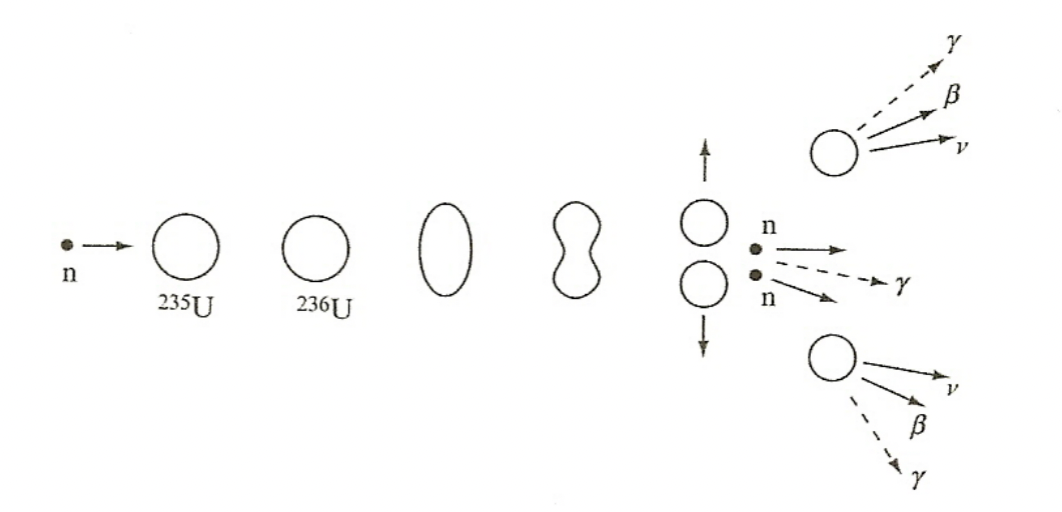 |
|||
| Fission Activation Energy | The energy required to overcome the fission barrier = deform | ||
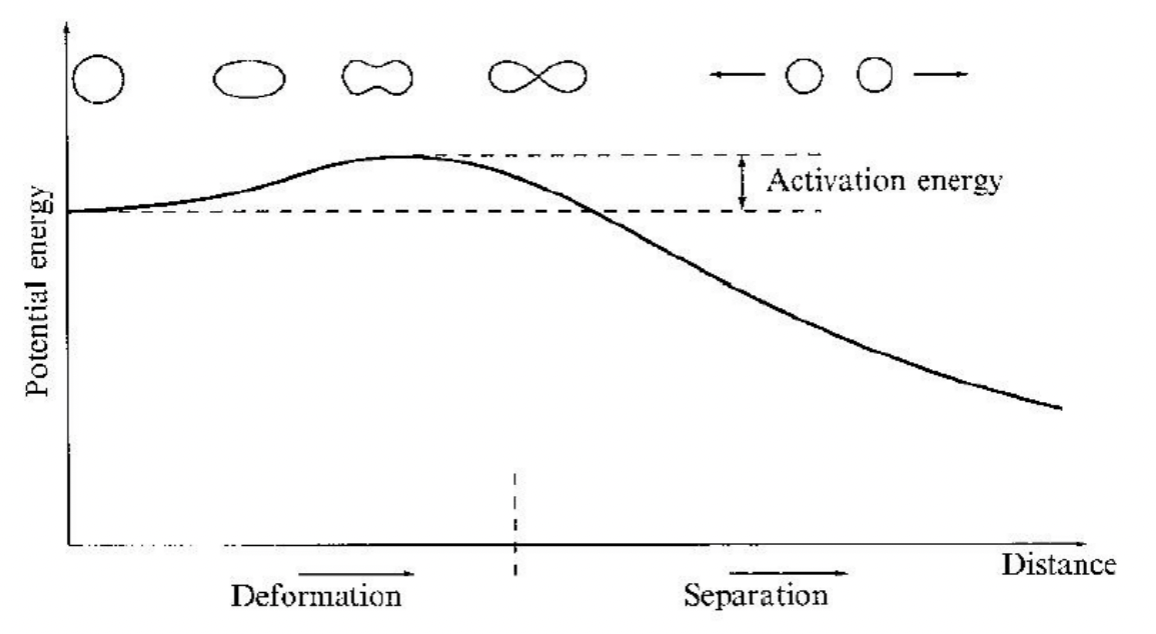 |
|||
| Properties of Fission | Energetically preferred to have one heavy group and one light group as fission fragment | 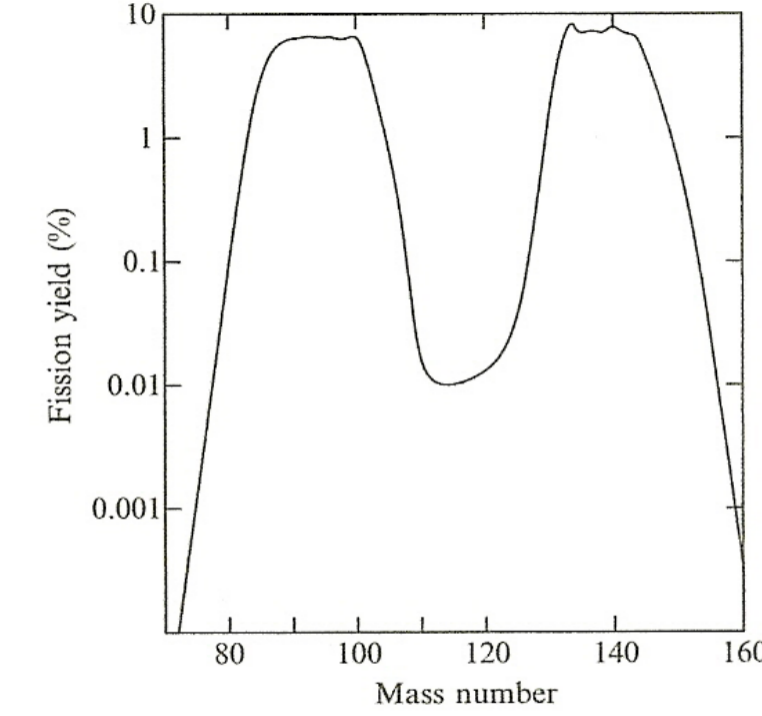 |
|
| When a fissionable nucleus absorbs a neutron and forms a compound nucleus, there is a competition between fission and gamma emission to release excitation energy, which doesn’t lead to fission | $\sigma_a = \sigma_f + \sigma_\gamma$ | ||
| Discovery of Neutron | James Chadwick found that if the energetic alpha particles emitted from polonium fell on certain light elements, specifically beryllium, an unusually penetrating radiation was produced (not gamma ray) | ||
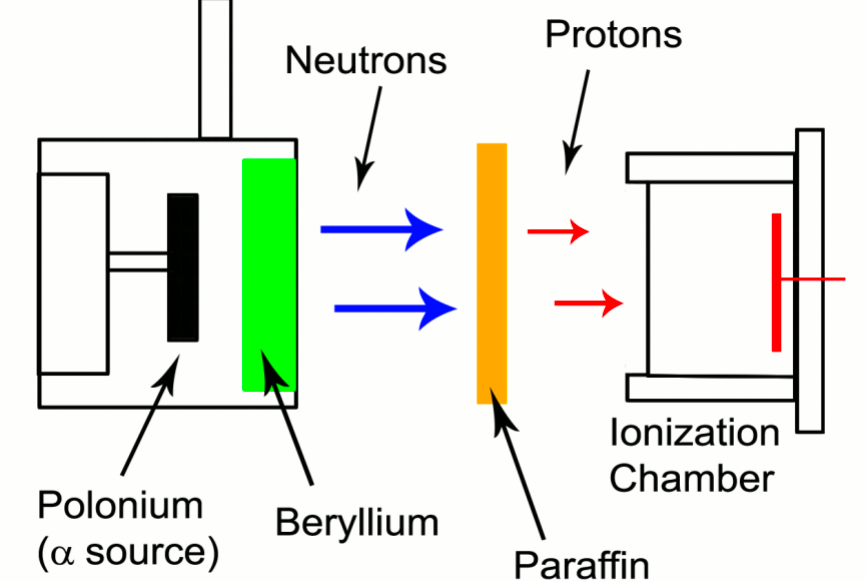 |
this radiation’s range, etc. can be measured by placing paraffin a distance away to perform (n,p) reaction | ||
| the first ‘weird’ event that happened about this was: Walther Bothe and Herbert Becker = discovered that when energetic α-particles from the decay of polonium impinged on certain light materials, they would eject high energy, very penetrating, neutral radiation; they thought they were γ-rays | 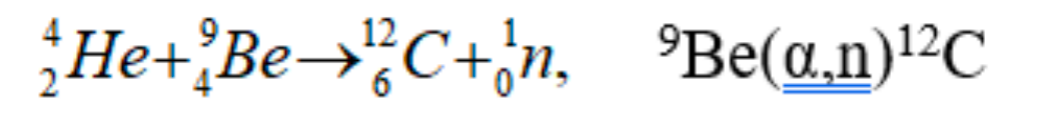 |
||
| ‘Discovery of Fission’ | Otto Hahn and Frederick Strassmann | ||
| Observed presence of barium and other middle-weight elements in a uranium sample bombarded by neutrons and noted large release of energy. | |||
| 12/2/1942 – Enrico Fermi – 1st controlled fission chain reaction in Chicago Pile 1 | |||
| Start of Nuclear Weapon | 7/16/1945 – 1st nuclear weapon test: Trinity in White Sands Proving Grounds, New Mexico. | ||
| called “The Gadget.” 20 kT (84 TJ). Pu implosion device | |||
| Types of Nuclear Weapons Mechanism | 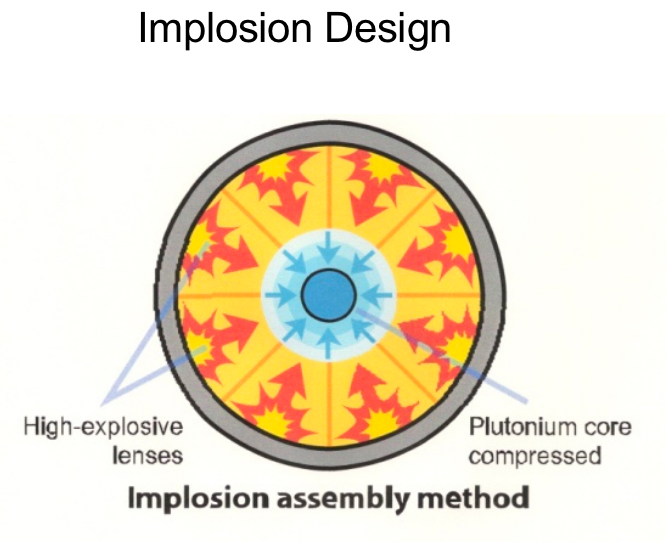 |
normal plutomium okay, but densely pressed is not = can go over critical mass | |
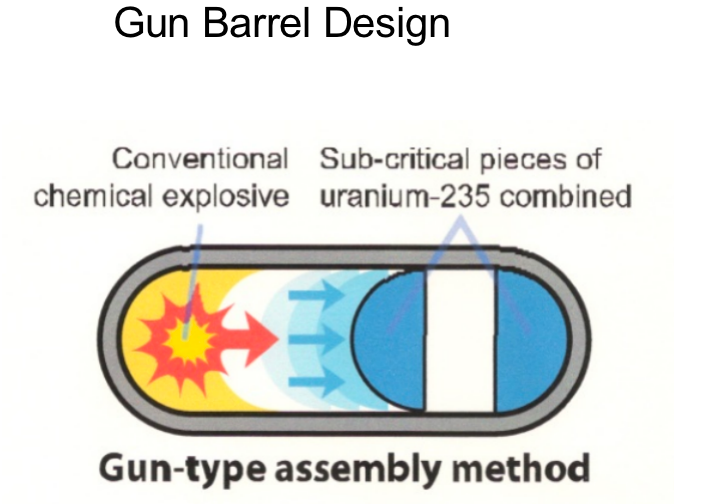 |
simply have separate halfs of sphere = explosion combine them = increase density = go react now it is uranium |
||
| Why no Pu+Gun Barrel? 1. Because plutonium is less dense than HEU, it would require a larger mass to reach criticality 2. even trace amounts of Pu-240 in the plutonium would release enough neutrons from spontaneous fission = wouldn’t explode but fizzle |
|||
| Nuclear Power Plant | 12/20/1951 – EBR-1, Idaho National Lab, Idaho Falls, Idaho. First generation of electric power from nuclear power plant | ||
| Delayed Energy and Delayed Neutrons | nuclear reactor core and spent fuel continue to emit considerable energy even after the nuclear chain reaction process has stopped. This happens because | ||
| 1. fission fragments as a by-product are themselves every radio-active = release energy | |||
| 2. delayed neutrons play a critical role in the control of nuclear fission reactions because they are emitted at a slower rate than prompt neutrons, which are emitted immediately following the fission event = helpful to make power change smoother = but still are neutrons | 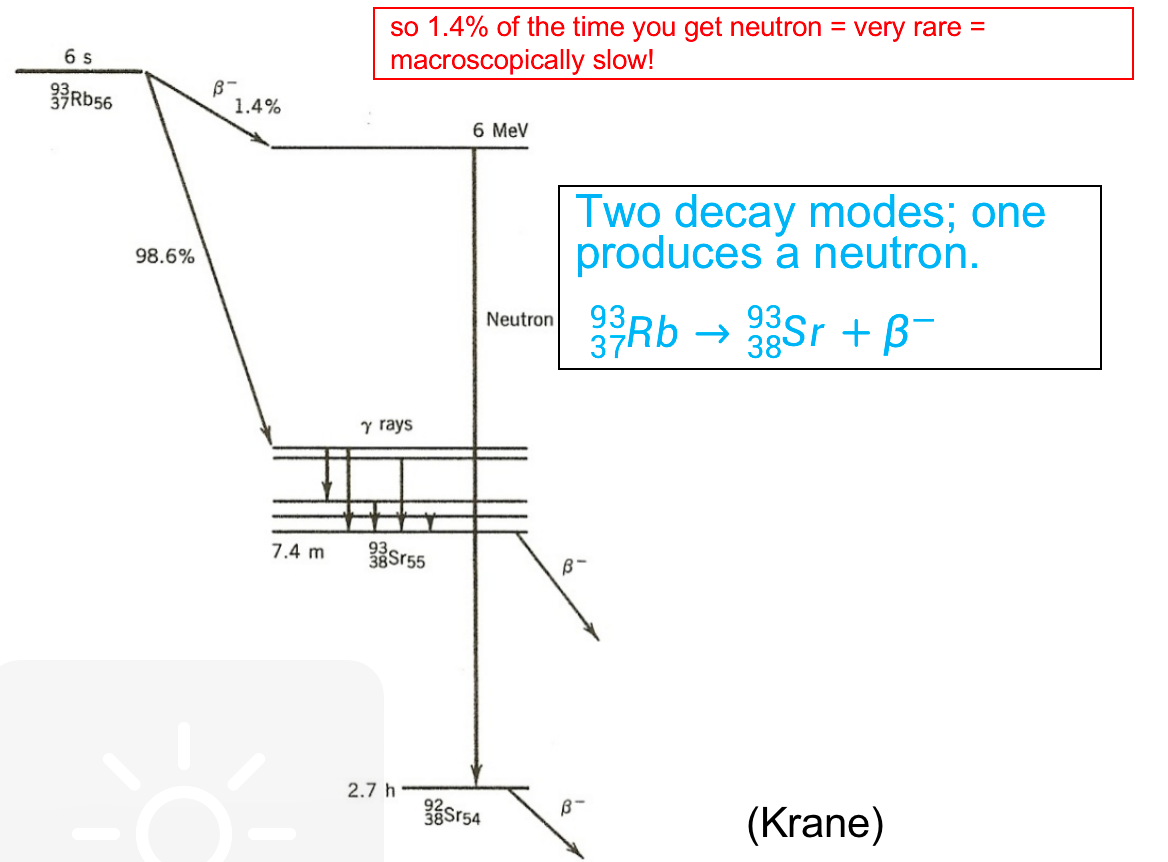 |
||
| Neutron Economics | each fission produces 2-3 neutrons of about 2MeV, but prompt fission neutrons must be thermalized to about 0.025 MeV | ||
| In the slowing down process, must avoid 1. absorption by other nuclei 2. leakage out of the system. |
|||
| 3. (uncontrollable) absorbed neutron but gave non-fission reaction | |||
| Chain Reaction | 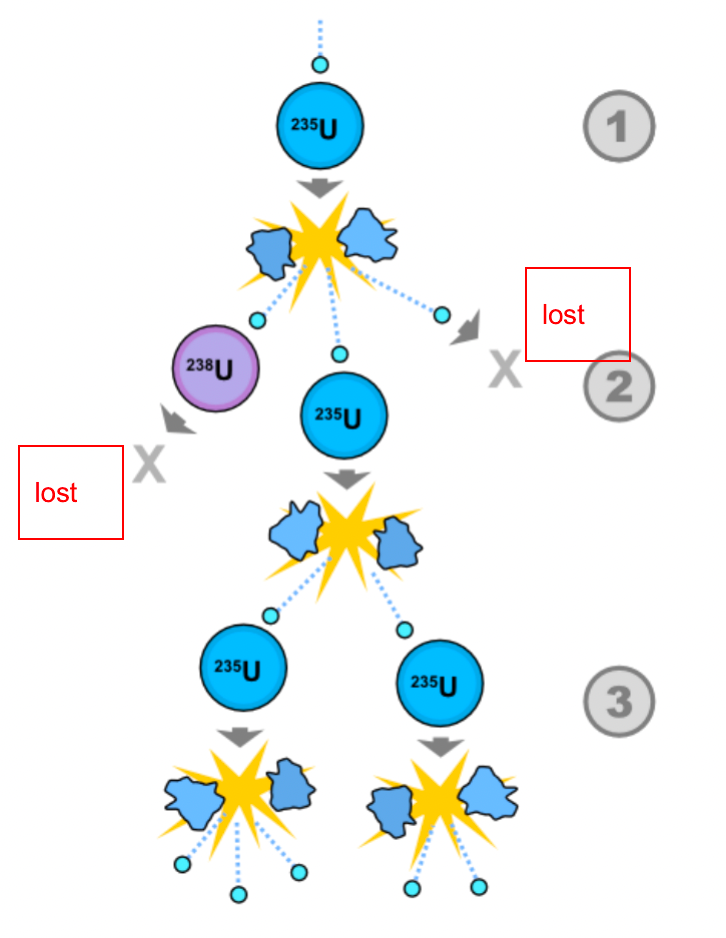 |
||
| Neutron Multiplication Factor | measure if your chain reaction is sustaining/increasing/decreasing | ||
 |
|||
 |
|||
 |
recall the section on neutron economics | ||
| Thermal Fission Factor | probability of a fission event occurring when a neutron collides with a nucleus | Not all neutrons absorbed in fuel cause fission | |
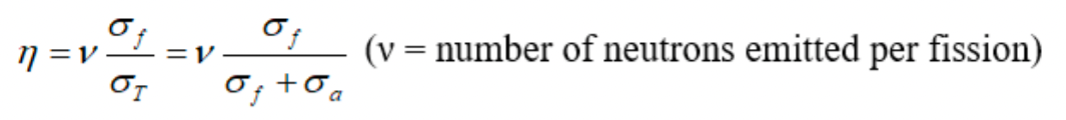 |
basically $\sigma_f + \sigma_a = \sigma_T$ | if 99.3% U-238 and 0.7% U-235, then the ratio is $\frac{0.7*\sigma_f(^{235}U)}{(0.7\sigma_T(^{235}U)+99.3\sigma_T(^{238}U))}$ |
|
| because only $^{235}U$ can fission = Most nuclear reactors and all nuclear weapons require higher U-235 enrichment | |||
| Methods for U-235 Enrichment | 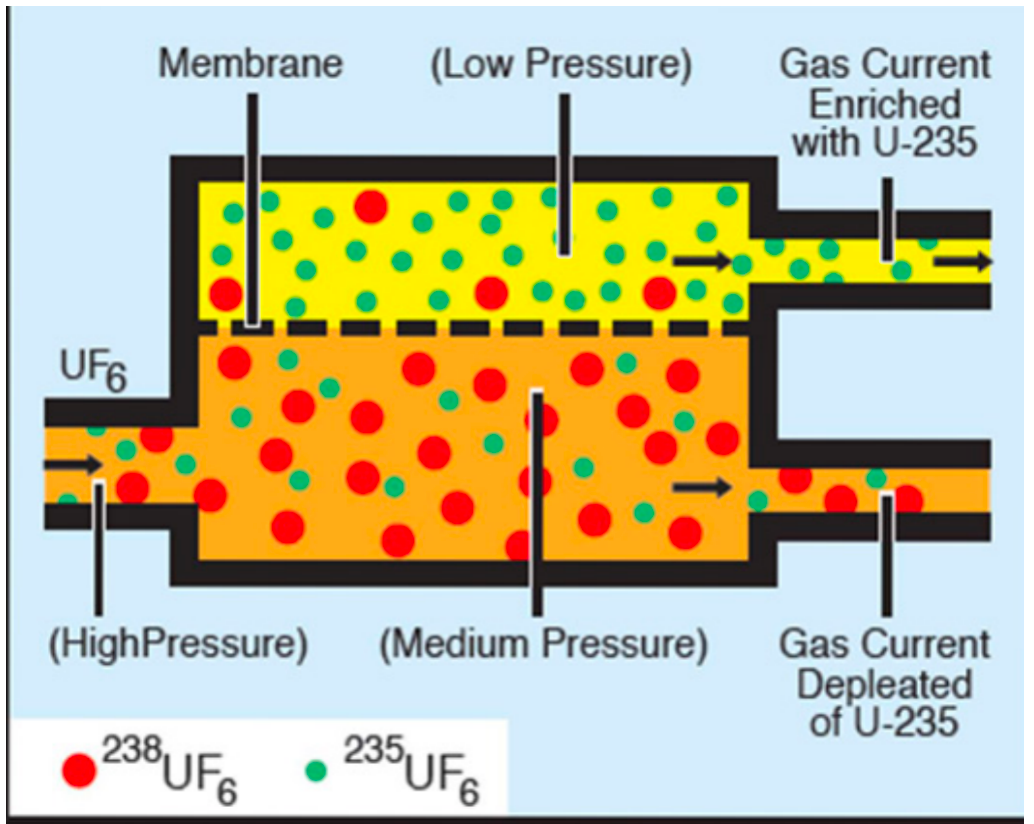 |
Gaseous Diffusion Enrichment: since U238 is a little bit heavier (cannot separate them chemically as they are the same, but physicaly not). Therefore smaller would go through more readily at the top | |
| and you can repeat this process over and over | |||
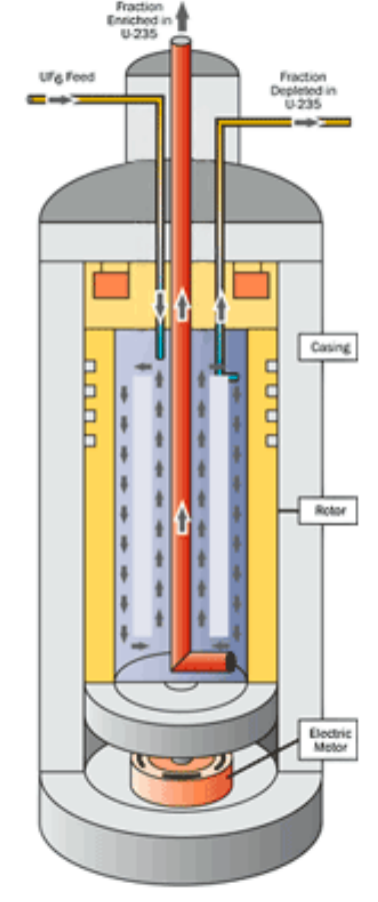 |
Gas Centrifuge Enrichment: again, U238 is a little bit heavier than U235, so another approach is to spin it very fast | ||
| Enrichment Definitions | LEU – Low Enrichment Uranium: < 20% U-235 | ||
| HEU – High Enrichment Uranium: > 20% U-235 | |||
| Weapons Grade Uranium: > 90% U-235 | |||
| Components in a Nuclear Power Plant | Fuel pellets – typically, sintered UO2 enriched to 3-5% in 235U. | Fuel pellets and fuel rods are both used to store and transport nuclear fuel in nuclear reactors. | |
| Fuel rods – typically, clad in Zircalloy to contain fission products and gases | |||
| Control rods – neutron absorbers among fuel assemblies | to regulate the number of neutrons available to sustain the chain reaction | ||
| Reactor core – typically, “square cylinder” shape | |||
| Coolant/moderator – light water most common | to slow down neutrons to thermal | ||
| Structural material – alloys of steel (absorber/reflector) | |||
| PWR and BWR | 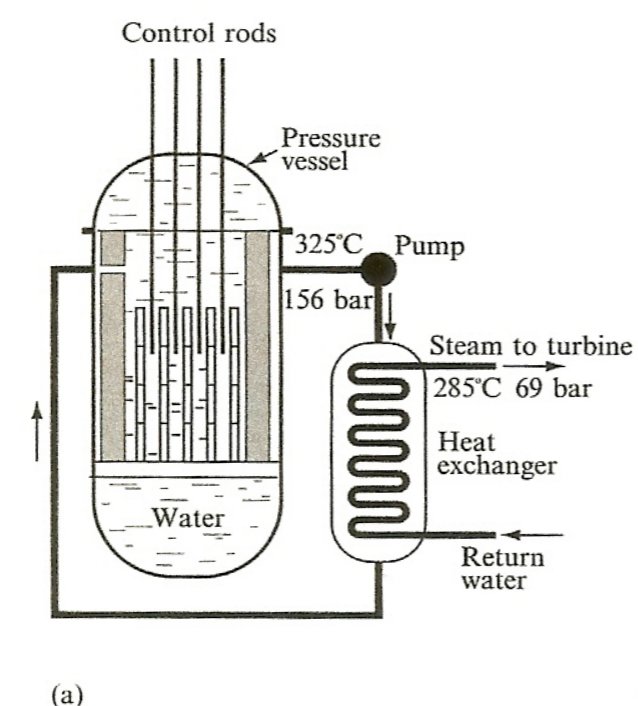 |
pressurized, transfer of heat energy | |
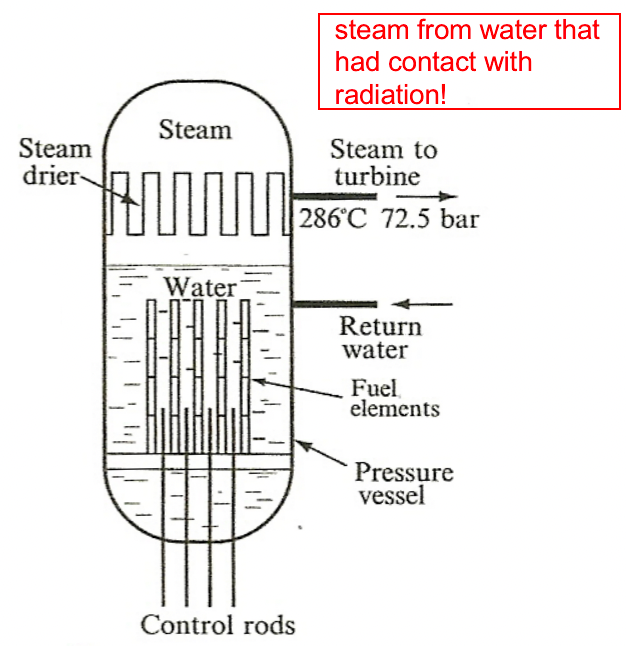 |
could have secondary radiation, but more efficient | ||
| PWR Schematic | 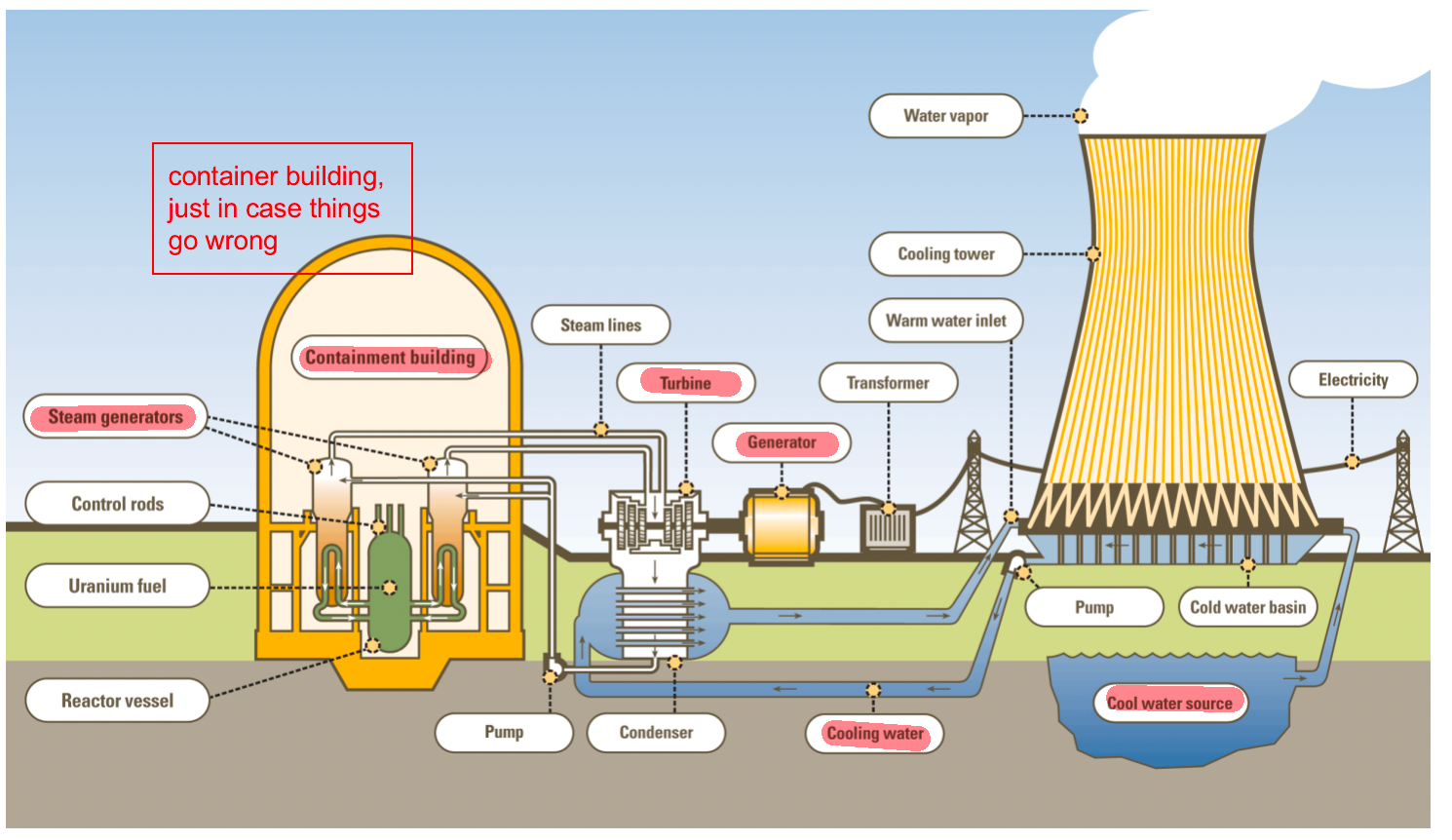 |
Fusion
Why could fusion be useful if we had fission already?
- much less radioactive waste
- but the major problem is it is technically harder
| Name of Concept/Equation | Definition/Equation | Notes | Example |
|---|---|---|---|
| Why is Fusion Energetic Useful? | 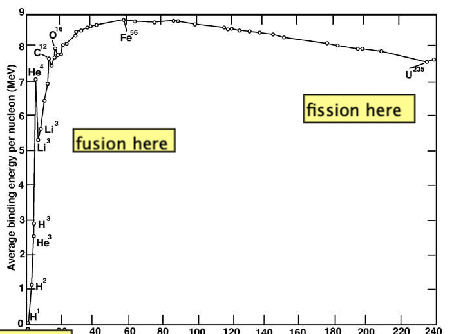 |
||
| Extra Requirement for Fusion | since nuclei are positively charged, so must impart high kinetic energies to the to overcome the repulsive Coulomb barrier = close enough for strong force to form new nucleus | ||
| 1. high temperature (i.e., kinetic energy) | |||
| 2. high density (close enough) | |||
| 3. confinement time: amount of time that the plasma must be confined in order for the reactions to occur | later on will see that density and confinement determines how much energy can be gained | 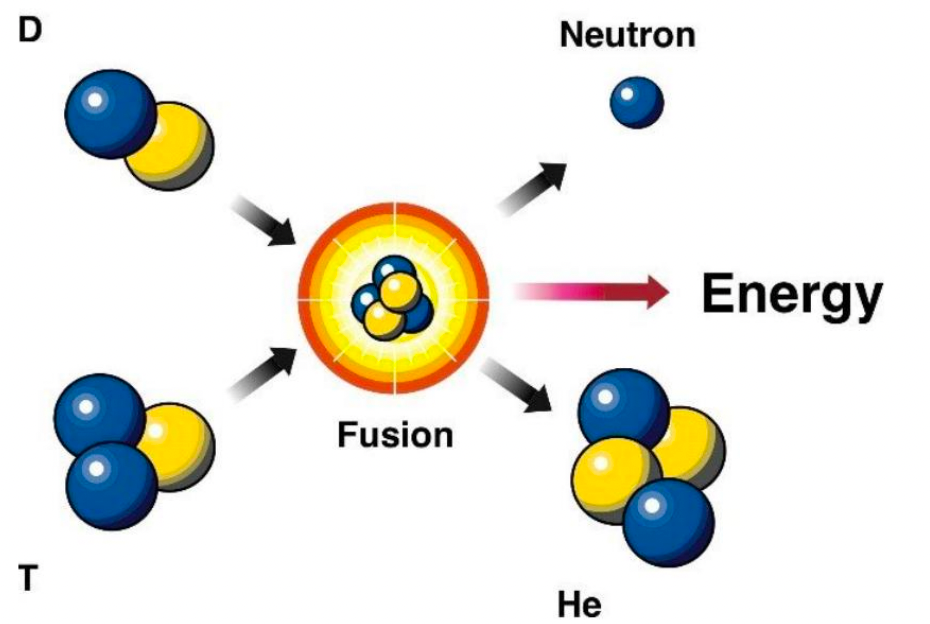 |
|
| Magnetic Confinement Basics | confine plasma using magnetic fields = quite complicated setup | because plasma = lot of charged particles in gaseous form | |
| works based on Lorentz Force | but will lose them if they move in parallel of the field! | ||
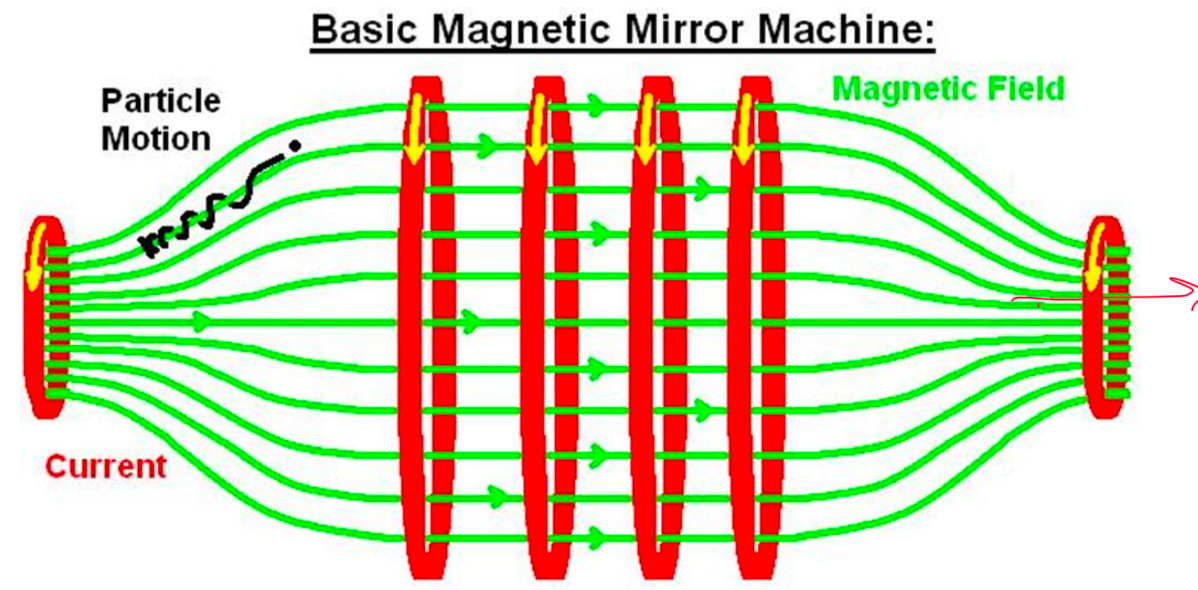 |
|||
| Inertial Confinement | Heat and fuse ions so rapidly that they do not have time to escape. | ||
| typically use laser beams to compress and heat fuel pellets. | |||
| Fusion Reaction Examples |  |
Most uses isotopes of hydrogen to minimize repulsion | |
| the highlighted ones have high cross section, and non-gamma energy release = can be more easily retrained | |||
| Helium as a product is very stable, hence releases a lot of energy! | |||
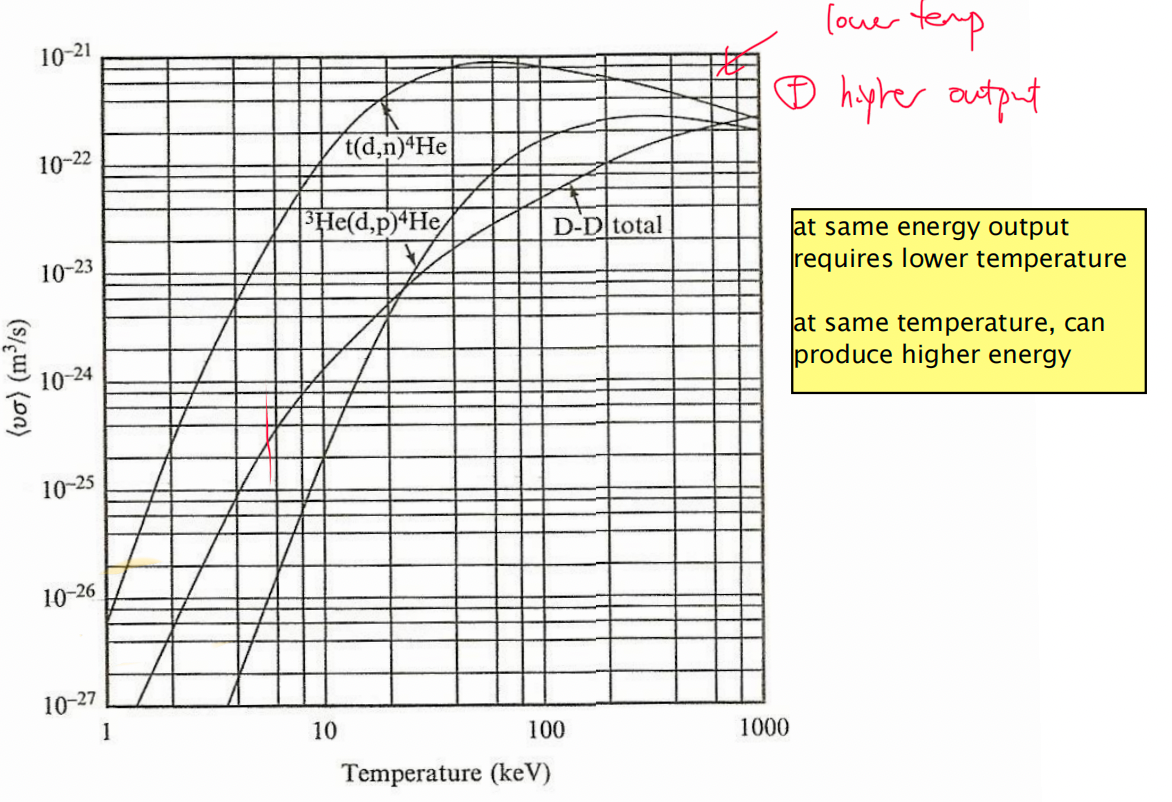
| Properties of DT Fusion Reactions | high cross section | ||
| produces a lot of energy | |||
| produces an alpha particle, which can be re-used to heat up the plasma | |||
| shield against neutrons, which are also very energetic | |||
| tritium (T) don’t occur naturally, so often need to be bred in the reactor factory | can be bred from Lithium | ||
| Why would DT be preferred? | 1. requires lower energy 2. produces more energy |
 |
|
| Reaction Rate of Fusion | Reaction prob per unit time = $n_2 \sigma v$ | $v$ speed of the particles $n_2$ is density of particle 2 |
|
| considers prob of particle 1 interacting with particle 2 | |||
| total reaction rate per unit volume: $R=n_1n_2\sigma v$ | |||
| $R=n_1n_2 \lang \sigma v \rang$ | since plasma = gas particles = velocity is defined by Boltzmann distribution | ||
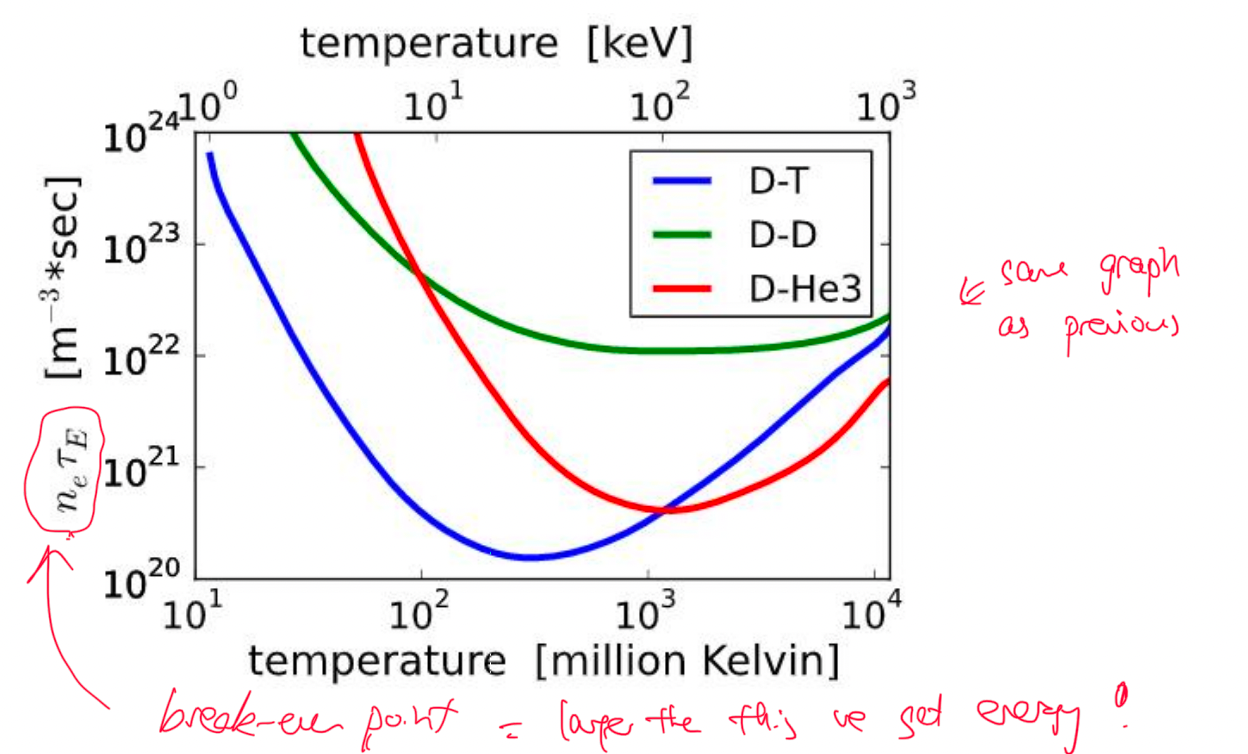
| Fusion Energy Output and Break-Even | Fusion energy output = $E_f=n_1n_2\lang \sigma v\rang Q \tau$ | $\tau$ is confinement time! $Q$ is energy released per reaction |
|
| also includes density $n_1,n_2$ | |||
| Break-Even $n\tau > \frac{12kT}{\lang v \sigma \rang Q}$ | Lawson Criteria: need to achieve this to get more energy out than input | ||
 |
|||
| Magnetic Bottle Confinement | 1. Closed-field geometry (e.g., torus) | ||
| 2. Toroidal field (TF) – Coils external and perpendicular to toroidal containment vessel generate TF | |||
| 3. Poloidal field (PF) – pass current around axis of torus. Compensates for weakening TF with increasing $r$ | 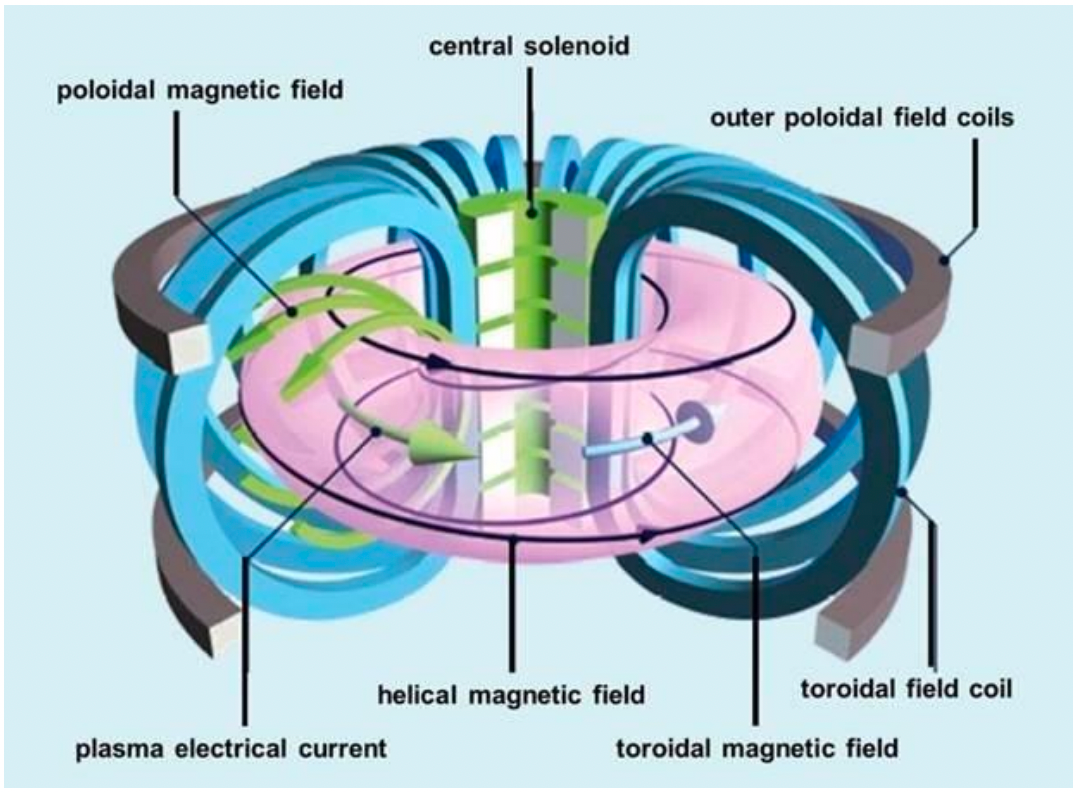 |
||
| Tokamak is one famous example! | |||
| Inertial Confinement Mechanism | 1. the energy from the laser or particle beam pulses is absorbed by the fuel target, heating it to extremely high temperatures and causing it to undergo a rapid expansion. | difficulty is to generate sufficient power to achieve this | |
| 2. This expansion creates a shock wave that compresses the fuel target, increasing the density and temperature of the plasma and creating conditions suitable for fusion reactions. | |||
| therefore, requires lasers and fuel pellets | |||
| National Ignition Facility | NIF: 192 laser beams focused onto small target, uses Indirect target | ||
 |
Laser pulse vaporizes the heavy metal case, generating intense x-rays inside the hohlraum, which compresses and heats the DT fuel | ||
| Hohlraum = the metal cylinder |
Final
- Nuclear sturcture
- spin has an effect on energy
- know every term in SEMF, what it represents
- pairing term
- vibrational harmnoics shapes
- nuclear potential energy
- Nuclear Instability
- gamma emission comes from nucleus, actually comes fro the daughter
- selection rules for gamma emission, including the table
- transition ratess
- Decay schemes
- high polarity and high half life
- internal conversion (eject electron)
- beta decay three possible transitions
- tell by excess protons or neutrons whether if it goes beta plus or beta minus
- alpha decay
- QM consideration that as long as Q is positive it will happen
- Nuclear Reactions
- classification
- scattering, inelastic scattering; knockout
- direct reactions and compound-nucleus decay
- cross section and density equation and reaction rate
- estimate the cross section such as assuming no coulomb interactions with $\pi R^2$; but with intearaction $\pi b^2$
- cross section calculation for charged particles
- no need to know partial waves
- compound nuclear reactions equation
- classification
- Fission
- binding energy curve and why fission is possible
- high cross section with thermal neutrons
- fission activation energy - when you pass the poit of this yuo can fission
- fission history and discovery of neutron
- chain reaction graph of uranium
- neutron multiplication factor
- reactors would want to stay at $k=1$, which is controlled by control rods
- why enrichment is needed
- nuclear reactor basics
- fuel pellets
- Pressurized WR and BWR designs; difference is that water doesn’t boil and goes into heat exchange
- Fusion
- why fusion is possible in binding energy curve
- but the hard part is to have a high temperature, etc.
- magnetic confinement v,s, inertial confinement: heating them so quickly
- reaction rate for fusion equation with $R=n_1n_2 \sigma v$
- triple product and lawson criterion
- toroidal fields, know stuff like this exists
- tokamak
- inertial confinement
- using lasers
- why fusion is possible in binding energy curve
-
some shared topisc shuch as alpha and beta decay
- Energy calculation, very practical