COMS3203 Discrete Math

Discrete Math Logistics

• Content on Courseworks, homework on Gradescope
• Notes on Coursework provided by the Professor. Additional examples (not on the book) will be gone over during classes.
• Recitations will be recorded, and content in the recitation needs to be studied
• Homework: weekly, needs to be typed

Logic

Propositional logic, truth tables, Boolean algebra, inference.

Axioms of Numbers

Natural Numbers contain all positive whole numbers (excluding zero)

\[\mathbb{N} = \{ 1,2,3,... \}\]

Even Numbers an integer $a$ if even IFF $a$ is divisible by 2; or exists an integer $b$ such that $a = 2b$

Odd Numbers an integer $a$ if is odd provided there exists a number $q \in \mathbb{Z}$ s.t. $a = 2q+1$

Prime Numbers let $p \in \mathbb{Z}, p>1$. We call a number prime provided it is only divisible by $1$ and itself.

• e.g. 2, 3, 5…. By definition $1$ is therefore not prime.

etc. Just to recall:

• $\mathbb{Z}$ represents integer, $\mathbb{Q}$ represents rational numbers (fractions with integer num/denom), $\mathbb{R}$ represents real numbers
• $\mathbb{N}\subseteq Z \subseteq Q \subseteq R$

Introduction to Logic

Proposition: a proposition is an objective, declarative statement that’s either true or false.

for example, proposition includes:

• $2+2=4$ (is true)
• $2 > 5$ (is false)
• $x+2=5$ (used in first order logic as it depends on $x$=a predicate, but it is a proposition)

not propositions:

• Newborns are cute (subjective)
• Hello.

Atomic Proposition: simplest (elementary) form of a proposition. Some common notations used to denote atomic proposition include $p,q,r,t,s,z$ etc.

Compound Proposition: a proposition constructed from two or more atomic propositions using connectives, or adding a connective to an atomic proposition.

Major Connectives in Propositional Logic: if we have a proposition $p$

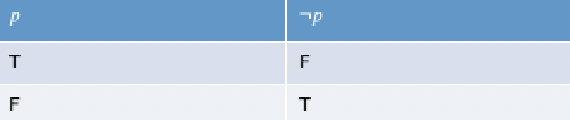
• negation (not): $\neg p$. For example, $p=$ it is snowing, $\neg p$ = it is not snowing. All possible negation actions include:

  

  note that the Truth Table above basically lays out all the possible “scenarios”

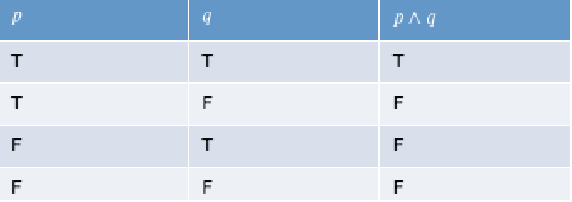
• conjunction (and): $p \land q$.

  

  now that there are 2 “variables”, we have $2^2$ possibilities

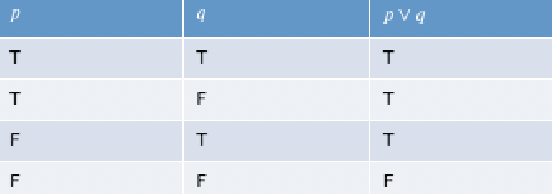
• dis-junction (or): $p \lor q$.

  

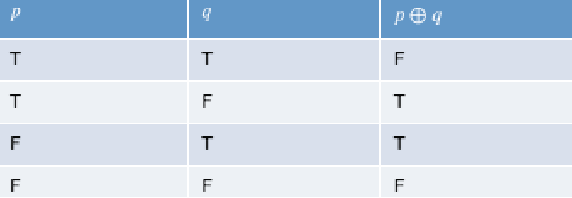
• exclusive or (xor). $p \oplus q$. You expect only one of the options. interestingly this is more related to using “or” in natural language: e.g. “you can either have $p$ as side dish or $q$”

  

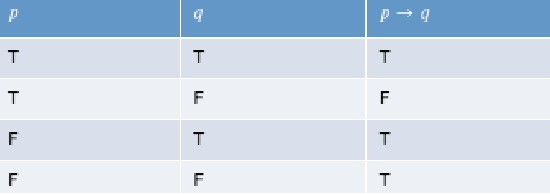
• implication (if, or implies): $p \to q$. For example, “if heavy snow ($p$), then Columbia is closed ($q$)”. So whenever $p$ is fulfilled, we expect $q$ to happen.

  

  the first two rows are straight-forward. Consider “If I get an A in this course ($p$), then I will give you a dollar ($q$)”.

  • If $p,q$ both happened, then I kept my promise. If $p$ happened but I didn’t give you a dollar ($\neg q$), then I broke the promise.
  • If $p$ didn’t happen in the first place, then technically I haven’t yet break the promise. In this case we assume it is still true, i.e. the benefit of doubt

• if and only if (iff) $p \iff q$. Basically this means a conjunction to two implications $(p \to q)\land (q \to p)$

  

  where the last one has $(p \to q)=T$ and $(q \to p)=T$ due to benefit of doubt. Hence $(p \iff q) = (T \land T) = T$. Notice that basically $p \iff q$ is true when $p,q$ are equivalently true or equivalently false.

note that

• every connective mentioned above except for negation are binary connectives.
• the order of evaluation would go from
  1. $()$ processed from inside to outside
  2. $\neg$ negation
  3. $\land$ and
  4. $\lor,\oplus$
  5. $\to$ implies
  6. $\iff$
  7. left to right

and in English

where the more tricky ones are highlighted.

• “$p$ only if $q$” means only if the consequence $q$ happens
• “$q$ is a necessary condition for $p$” means “$q$ is a necessary conclusion for $p$”
• a trick can be to consider which one maps correctly to “if $p$ then $q$”.

---

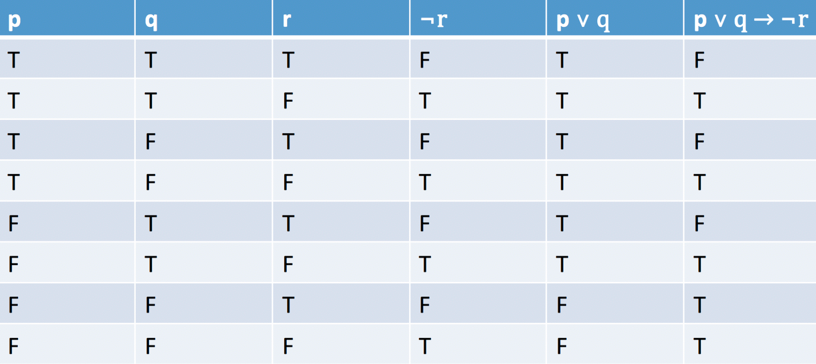
For Example, consider $p \lor q \implies \neg r$.

First of all, how many rows will there be? Since there are three variables, $2^3=8$ rows.

---

Implication can be very tricky when combined with negation:

• negation of implication: $\neg (p \to q)$ is $p \land \neg q$.

  • for instance $\neg$(hit$\to$hurt) is (hit$\to\neg$hurt)
  • is proven below (of course, they don’t come out of nowhere. See the example in the proof)

• if $p\to q$ is implication, then

  • converse $q \to p$
  • contrapositive $\neg q \to \neg p$
  • inverse $\neg p \to \neg q$

  why they are named like this can be seen more clearly from the truth table:

  p	q	$p \to q$	$q\to p$	$\neg q \to \neg p$	$\neg p \to \neg q$
  T	T	T	T	T	T
  T	F	F	T	F	T
  F	T	T	F	T	F
  F	F	T	T	T	T

  notice that $p \to q$ is the same as $\neg q \to \neg p$, and $q\to p$ is the same as $\neg p \to \neg q$.

Logical Equivalence: two propositions $p,q$ are called logical equivalent provided they have the same truth table

\[p \equiv q,\quad \mathrm{or}\quad p=q\]

we will mostly use $\equiv$. Note that this is not a connective, but rather a relation.

Now you can show that $\neg (p \to q) \equiv p \land \neg q$

p	q	$p \to q$	$\neg (p \to q)$	$p\land \neg q$
T	T	T	F	F
T	F	F	T	T
F	T	T	F	F
F	F	T	F	F

And similarly, you can show that:

\[p \to q \equiv \neg p \lor q \equiv \neg q \to \neg p\]

So implication is just a disjunction! This is very important to know!

• e.g. if I hit my thumb, it will hurt $\equiv$ I don’t hit my thumb, or else it will hurt

Tautology: a proposition is always true is called a tautology. For example, $p \lor \neg p$ is a tautology as no matter what value $p$ takes, every row in the truth table is true.

A more interesting example would be

• you may feel this is similar to $\iff$. But $\equiv$ is a relation between propositions, whereas $\iff$ is a connective.
• e.g. we know $p\to q \equiv \neg p \lor q$ as they have the same truth table. Then this also mean $(p\to q) \equiv (\neg p \lor q)$ is a tautology

Fallacy/Contradiction: a proposition that is always false. For example, $p \land \neg p$.

Contingency: a proposition that is not a tautology or fallacy, i.e. is a valid proposition. Usually we can just call this a (valid) “proposition”.

---

For Example: Wason Puzzle

Consider a set of four cards. Each card has a letter on one side and one number on the other side.

Consider the proposition: “If there is a vowel on one side, then there is an even number on the other side.”

Question: What are the only cards that you need to turn to check if the proposition is True or False?

Answer: you only need to turn $A$ and $3$. Let $p$=is vowel and $q$=other side is even. To falsify it, we need to basically get (vowel and not even) because this is the only case the implication $(p\to q)=F$. Therefore, the two relevant checks will be $p=T$ and $q=F$, corresponding to the card $A$ and card $3$.

More interestingly, notice that checking $3$ is the same as the $\neg q \to \neg p$ which is the contrapositive!

Laws of Propositional Logic

These basic laws (equivalences) are important as:

• can be used to show that a proposition is equivalent than other ones, a tautology, of fallacy
• simplify a proposition

where the most important ones are highlighted. Most of them has something to do with simplifying $\land$ and $\lor$

• associativity: has to be used on the same connective (e.g. $(p\lor q)\land r$ has to be done in a distributive case)
• distributivity: you can also show that $(q \lor r) \land p \equiv (q \land p) \lor (r \land p)$ by using the commutativity law and the first row in Distributive law
• absorption: note that this is different from “Idempotence law”
• DeMorgan’s: how to distribute negation

Proof of $p \lor (p \land q) \equiv p$.

To get only $p$ on the RHS, we can consider $p \land T = p$ or $p \lor p = p$ as the last step. Here we use the first one:

\[p \lor (p \land q) = (p \land T) \lor (p \land q) = p \land (T \lor q) = p \land T = p\]

Proof of $p \land (p \lor q) \equiv p$

\[p \land (p \lor q) = (p \lor F) \land (p \lor q) = p \lor (F \land q) = p \lor F = p\]

which we already know is $p$ from the previous proof.

---

For Example: show that

\[(p \lor q) \land (p \lor \neg q) \quad \text{is a tautology}\]

Proof: (first you start intuitively), realize that you are “or”ing $q$ and $\neg q$, hence:

\[(p \lor q) \land (p \lor \neg q) = p \lor ( q \land \neg q) = p \lor (T) = T\]

Logical Inference

Or logical deduction.

Logical inference/argument: a sequence of propositions such that:

• all but the last propositions are called premises (i.e. precedes conclusion)
• the last proposition ($q$) is called conclusion

\[\frac{p_1p_2,\dots p_n}{q}\]

an argument is called valid if the premises imply the conclusion. This means that:

\[(p_1 \land p_2 \land \dots \land p_n) \to q \equiv T \quad \text{(is a tautology)}\]

But notice that implication has the benefit of doubt, so it only makes sure that if all $p_i$ is satisfied, $q$ will happen. If one of the $q_i$ is false, it does not affect anything.

---

For Example:

\[\frac{p_1p_2}{p_1 \land p_2} \quad \text{is valid}\]

because it is basically $p \to p$. In fact, if you have equivalence, such as

\[\text{both}\quad \frac{\neg \neg p}{p},\frac{p}{\neg \neg p}\quad \text{are valid}\]

you can also see that via a Truth Table

---

Rules of Inference

• addition:

  \[\frac{p}{p \lor q}\]

  you can prove this by showing that $p \to (p\lor q) \equiv T$

  \[\neg p \lor (p \lor q) = T \lor q = T\]

  e.g. “it is raining” concludes “it is raining or xxxx” is obviously true.

• conjunction:

  \[\frac{p \quad q}{p \land q}\]

  basically means $(p \land q) \to (p \land q)$

• simplification:

  \[\frac{p \land q}{p}\text{ and } \frac{p \land q}{q}\]

  because $p \land q \to p \equiv T$

• disjunctive syllogism:

  \[\frac{p \lor q \quad \neg p}{q}\]

  proof is left to you as an exercise, but intuitively if the premises is true, then it means $p$ is false hence $F \lor q$ is true concludes $q$ is true.

• hypothetical syllogism:

  \[\frac{p \to q \quad q \to r}{p \to r}\]

  which implies that implication is transitive.

• resolution

  \[\frac{p \lor q \quad \neg p \lor r}{q \lor r}\]

  meaning that if $p\lor q$ and $\neg p \lor r$ is true, then it means either $q$ or $r$ has to be true. Hence the conclusion $q\lor r$ is true. You can again try to prove this formally $((p \lor q) \land (\neg p \lor r) \to q\lor r) \equiv T$

• modus ponens (latin: mode that affirms)

  \[\frac{p \quad p \to q}{q}\]

  is a very important law, as it means if $p \to q$ is true and $p$ happened, then $q$ must conclude.

• modus tollens (latin: mode that denies)

  \[\frac{\neg q \quad p \to q}{\neg p}\]

  very similar as above, as it means if $p \to q$ is true (e.g. raining $\to$ take umbrella) and $q$ did not happen (e.g. did not take umbrella), then $p$ did not happen (e.g. it is not raining).

• transitivity this will be used a lot in proofs, so that basically if

  \[\frac{p}{q},\quad \frac{q}{r}\quad \text{are valid}\]

  then

  \[\frac{p}{r}\quad \text{is valid}\]

Inference is like implication except that it is (saying, since the premises are true, then this conclusion must be) always true

All laws of logic seen earlier can be written as rule of inference.

For example, you can transform $p \lor T \equiv T$ to inference as:

\[\frac{p \lor T}{T} \text{ and } \frac{T}{p \lor T}\]

Another example: premise $p_1$=It’s not rainy but it’s nicer than yesterday. $p_2$=we will watch a movie only if it’s raining. $p_3$ we will go swimming if we do not watch a movie. $p_4$=if we go swimming, we will be home after sunset.

1. Translate this into propositional logic (PL).

   let us use

   \[r:\text{rainy}\quad n:\text{nicer}\quad w:\text{watch}\quad h:\text{home}\quad s:\text{swim}\quad\]

   therefore this means

   • $p_1 = \neg r \land n$
   • $p_2 = w \to r$
   • $p_3 = \neg w \to s$
   • $p_4 = s \to h$

2. Show that these premises lead to “we will be home after sunset” (premises are “true”)

   1. first, we can simplify to get it is not raining:

      \[\frac{\neg r \land n}{\neg r}\]

   2. then applying modus tollens

      \[\frac{w \to r \quad \neg r}{\neg w}\]

   3. then applying modus ponens

      \[\frac{\neg w \to s \quad \neg w}{s}\]

   4. finally

      \[\frac{s\quad s\to h}{h}\]

Another Example: consider the whompus world where there are breezes $B$, pits $P$, and whompus $W$ such that $B_{11} \iff P_{12} \lor P_{21}$. And given that $\neg B_{11}$, show that $\neg P_{12}$

1. we can break up the iff into $P_{12} \lor P_{21} \to B_{11}$ by simplification

2. then apply modus ponens

   \[\frac{\neg B_{11}\quad P_{12} \lor P_{21} \to B_{11}}{\neg (P_{12} \land P_{21} )}\]

3. De Morgans law gives this means

   \[\neg (P_{12} \land P_{21}) = \neg P_{12} \land \neg P_{21}\]

4. finally, apply simplification

   \[\frac{\neg P_{12} \land \neg P_{21}}{\neg P_{12}}\]

First Order Logic

What if you want to say “there is no $W$ anywhere in the 5x5 cave”? Given current tools, this is not very convenient to do.

First Order Logic (abbreviated as FOL), also known as predicate logic, combines quantifiers and predicates for a more powerful and compact formalism. So in a sense, PL is a subset of FOL.

The idea is to:

• instead of having just $p$, we consider $p(x)$, or $p(x,y)$, etc (i.e. predicates)
• and we add quantifiers such as $\forall, \exists$

Predicate: A predicate is a proposition whose truth value depends on one or more variables.

N-ary predicate: a predicate with $N$-variables

\[\text{predicate}(\underbrace{x,y,z,...}_{\text{n variables}})\]

For example, this includes

• (predicates) $x+2=5$; even$(x)$; $x+y > 10$

• i.e. they can be true or false, but it depends on the values of the variables

• i.e. it is like a function that always evaluates to true or false given the “input values”

Quantifiers

• universal quantifier: $\forall$ expresses such as “for all, for every, all of, for each, for any, any of, given any, for an arbitrary, etc.”
• existential quantifier: $\exists$ expresses such as “there exist, for some, for at least one, there is, there is at least one, etc.”

Universal Quantifier additionally requires a variable name and a domain.

\[\forall \underbrace{x}_{\text{variable}} \underbrace{ \in A}_{\text{a domain}}\]

then this can be combined with a proposition

\[\forall \underbrace{x}_{\text{variable}} \underbrace{ \in A}_{\text{a domain}}\,\,(\text{predicate}...)\]

and then you can say something like “all aliens are green”, by considering $A$=the set of aliens:

\[\forall a \in A\,\, (green(a))\]

(which may or may not be true). Another example: all integers are even:

\[\forall a \in \mathbb{Z}\,\, (x\,\text{mod }2 = 0)\]

One powerful/additional feature of FOL is that your predicate can contain essentially functions, introducing many new operators such as “mod”, “equality”, etc.

More examples: “All Aliens are green and nice. Domain: Alien denoted $A$”

\[\forall a \in A \quad (\text{green}(a) \land \text{nice}(a))\]

Existential Quantifier: he existential quantifier, denoted with the symbol $\exists$, expresses the statements: there exist, for some, for at least one, there is, there is at least one, etc. The application of this is the same as the “Universal Quantifier”

For example: There exists an integer that is both even and prime

\[\exists x \in \mathbb{Z} \quad (\text{even}(x) \land \text{prime}(x))\]

but how do we prove it? In this example, we can by just realizing that $x=2$ satisfies. But in general, see FOL Statements and Proofs

Negation of FOL statements:

• $\neg (\forall x \quad p(x))$ means $\exists x \quad (\neg p(x))$
• $\neg (\exists x \quad p(x))$ means $\forall x \quad (\neg p(x))$

For example:

\[\neg(\forall x \exist y\quad p(x,y)) \equiv \exists x \forall y \quad\neg p(x,y)\]

where we abbreviated $\forall x (\exist y\quad p(x,y))$ to just $\forall x \exist y\quad p(x,y)$

Distributivity of FOL: in short, they do not distribute

• consider $\forall$:

  \[\forall x \quad P(x) \lor Q(x) \neq (\forall x \quad P(x)) \lor (\forall x \quad Q(x))\]

  e.g. consider $P(x)$=even(x) and $Q(x)$=odd(x). Then LHS = $T$, but RHS = $F\lor F=F$

• consider $\exists$:

  \[\exists x \quad P(x) \land Q(x) \neq (\exists x \quad P(x)) \land (\exists x \quad Q(x))\]

  e.g. consider $P(x)$=prime(x) and $Q(x)$=notprime(x). Then LHS=$F$ but RHS=$T\land T=T$

Domain of FOL

On the importance of the domain:

• Suppose you want to express: “All birds fly”

  \[\forall b \in B\quad \text{fly}(b)\]

• “All birds except penguins fly”. Naively:

  \[\forall b \in B \quad (\text{fly}(b)\land \neg \text{penguin}(b))\]

  but this also means we are stating two things:

  \[[\forall b \in B \quad \text{fly}(b)]\quad \land \quad [\forall b \in B \quad \neg \text{penguin}(b)]\]

  i.e. whenever $b$ is a penguin, this will be false $\neq$ our original statement. The correct way to express it is

  \[\forall b \in B \quad ( \neg \text{penguin}(b) \to \text{fly}(b) )\]

  i.e “if it is not a penguin, then it flies”, i.e. the only false case is “not penguin, and can’t fly”, and we are not claiming anything else than that, which is consistent with the statement.

  • (optional) technically you can also interpret this as “penguins don’t fly”. Then you might have

    \[\forall b \in B \quad ( \neg \text{penguin}(b) \iff \text{fly}(b) )\]

  • one way to think about this type of problem is to convert it into code

    for b in birds:
        if not (penguin(a)):
            fly
        # technically done
        # optionally:
        if penguin(a):
            not fly
    

Another example:

• “In the set of animals, all lions are fierce”

  \[\forall a \in A \quad \text{lion(a)} \to \text{fierce}(a)\]

• “some lions are fierce”

  \[\exists a \in A \quad (\text{fierce}(x) \land \text{lion(a)})\]

  is now correct.

Note: this means usually

• $\forall$ goes with $\to$ implications (because $\forall$ is a strong quantifier)
• $\exists$ goes with $\land$ conjunctions

For example: Consider the domain of Humans, you want to express “All kids has pets”

\[\forall h \in H\quad \text{kid}(h) \to \text{has pet}(h)\]

then another way to do this is

\[\forall h \in H ( \text{kid}(h) \to \exists \underbrace{ a \in A \quad \text{pet}(a) \land \text{is his pet}(a,k)}_{\text{exists a pet that the kid has}})\]

For example: “there exists a class that’s taken by every student”. Consider two domains, “event” (e.g. classes, workshops, conferences, sport events, etc) and “students”

\[\exists e \in \text{event}\quad \text{class}(e) \land (\forall s \in \text{students} \quad \text{take}(s,e))\]

Mixing Quantifiers

Consider the statement “All integers are even”, and

\[\forall x \in \mathbb{Z}\quad ( \exists y\in \mathbb{Z}\quad x=2y )\]

which is like a "nested loop" of, taking a loop over $x \in \mathbb{Z}$, and each is a even number.

Another example: what are the differences between:

• $\forall x \in \mathbb{Z}\quad ( \forall y\in \mathbb{Z}\quad x+y=0 )$ is false as, given an $x$, I can easily find a $y$ such that it does not hold
• $\forall x \in \mathbb{Z}\quad ( \exists y\in \mathbb{Z}\quad x+y=0 )$ is true, by picking $y = -x$ for any given $x$
• $\exists x \in \mathbb{Z}\quad ( \forall y\in \mathbb{Z}\quad x+y=0 )$ is false, as this says “given a $x$”, all $y+x=0$ for any $y \in \mathbb{Z}$
• $\exists x \in \mathbb{Z}\quad ( \exists y\in \mathbb{Z}\quad x+y=0 )$ is true

FOL Statements and Prelude to Proofs

Consider we want to prove:

1. $\forall x \in D\quad p(x):true$ means that $p(x)$ for all elements in $D$
2. $\forall x \in D\quad p(x):false$ means that there is at least one element for which $p(x)$ is false
3. $\exists x \in D \quad p(x): true$ means there is at least one element in $D$ for which $p(x)$ is true
4. $\exists x \in D \quad p(x):false$: means that for all elements in the domain $p(x)$ is false

This means that:

	$\forall x \quad p(x)$	$\exists x \quad p(x)$
Prove	prove such as proof by contradiction, induction, etc.	enough to find an example
Disprove	enough to provide a counter example	prove that $\forall x$ the predicate $p(x)$ is false, using …

Note that sometimes when a domain is “clear”, instead of $\forall x \in A\quad p(x)$ you can just write $\forall x \quad p(x)$.

For example: consider the FOLs, for which we will prove

1. “Any even integer is divisible by 2”. Let domain be $\mathbb{Z}$

   \[\forall x \in \mathbb{Z}\quad (\text{even}(x) \implies 2|x)\]

   where $2\vert x$ means 2 divides x. Note that technically “if it is divisible by 2, it is an even integer” is also true, so technically $\iff$ here would be correct. But since we are focused on proofs, we might not want to do extra work, i.e. prove both sides if using $\iff$.

2. “An integer is even iff it is divisible by 2”

   \[\forall x \in \mathbb{Z} \quad (\text{even}(x) \iff 2|a )\]

3. “The sum of two even integers is an even integer”

   \[\forall x,y \in \mathbb{Z} \quad (\text{even}(x) \land \text{even}(y)) \implies \text{even}(x+y)\]

   but don’t you need to specify that $\text{even}(x,y)$ is also an integer? This is not necessary here by the axiom of closure property (adding two elements in $\mathbb{Z}$ results still in $\mathbb{Z}$).

4. “Let $r\in \mathbb{R}$. If $r$ is irrational, then $\sqrt{r}$ is also irrational”. We are allowed to also use the set of rationals $\Q$

   \[\forall r \in \mathbb{R} \quad (r \notin \Q \to \sqrt{r} \notin \Q)\]

5. “If $x$ is even, then $x^2+x$ is even.” Domain is integer.

   \[\forall x \in \Z \quad (\text{even}(x) \to \text{even}(x^2+x))\]

6. “There are no pair of integers that satisfy the expression $5x+25y = 1723$”

   \[\neg (\exist x,y \in \mathbb{Z}\quad 5x+25y=1723)\]

   or alternatively you can say

   \[\forall x,y \in \mathbb{Z}\quad 5x+25y\neq 1723\]

Challenge question: there exists a unique with the quantifier we already have, to express

\[\exists ! x \quad p(x)\]

where $\exists !$ is used now as a shortcut to express exists a unique

\[\exists x \quad p(x) \land (\forall y \quad p(y) \to (y = x))\]

this hints at, to prove a uniqueness theorem, you just need to show that: 1) there exist a solution, and 2) any other working solution is the same as that solution.

Note that it would be incorrect in this case to say

\[\forall x \quad p(x) \implies (\forall y \quad p(y) \to (y = x))\]

because then, it could be there is no such $x$ such that $p(x)$, i.e. the “exist a solution” part we wanted to express is no longer there!

Proofs

First we need to define a few jargon

Axiom: An axiom is a proposition that is assumed to be True. You don’t need to prove them.

Lemma: A preliminary mathematical proposition for which there is/needs a proof. Generally, lemmas precede a bigger result and lay the ground to a theorem.

• a baby version of “theorem”, but still requires a proof

Theorem: A declarative mathematical statement for which there is/needs a proof

• in greek this means “something needs to be proved”

Corollary: A proposition that follows from a theorem in just a few steps.

• i.e. once the theorem is proven, these come very naturally/can be proven easily

Conjecture: A strong mathematical result that is strongly believed to be true, but is yet to be proven.

In general, you will be approaching them with:

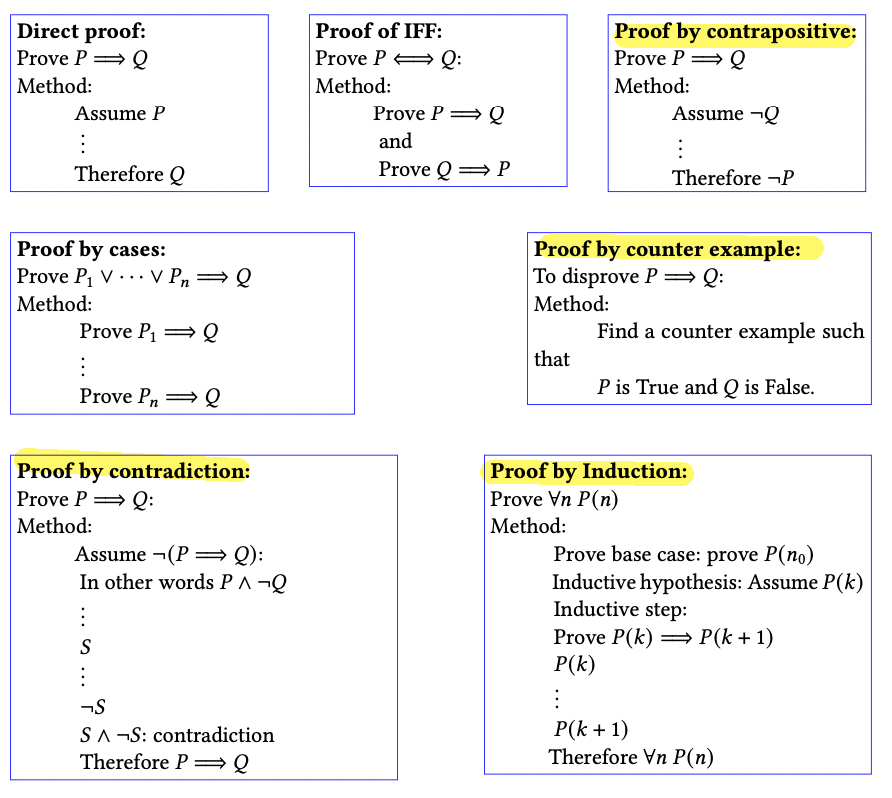
Proof by Enumeration

When the domain is small, we can verify the proposition for all values.

For Example: Proposition $\forall x \in \mathbb{Z}$ then $1 < x < 5 \implies (2\vert x) \lor (3\vert x)$

Proof: we consider for each case $1<x<5$

1. when $x=2$, $2\vert x$ hence is true
2. when $x=3$, $3\vert x$ is true hence true
3. when $x=4$. $2\vert x$ is true hence true

Direct Proof

Given a statement

\[\forall x \in D\quad p(x) \implies q(x)\]

Then in a direct proof you basically

Directly prove $p \implies q$ using definitions/axioms/logic. I.e. assuming $p$ is true, then $q$ is true.

For Example: $\forall a \in \mathbb{Z}$ and $\forall b \in \mathbb{Z}$ then

\[\text{$a$ is even } \land \text{ $b$ is even } \implies (a+b) \text{ is even}\]

Proof: since we know $\text{$a$is even } \land \text{$b$is even }$

1. this implies

   \[\exists k \in \mathbb{Z},\quad a=2k\\ \exists z \in \mathbb{Z},\quad b=2z\]

2. hence this means

   \[a+b = 2(k+z)\]

3. hence this means

   \[\exists t \in \mathbb{Z},\quad (a+b)=2t\]

   e.g. by picking $t = (k+z)$

4. therefore $(a+b)$ is even

Recall that (we will use this quite often)

• $x$ is even $\iff$ $2\vert x$, or $\exists k \in \mathbb{Z},\ x = 2k$
• $x$ is odd $\iff$ $\neg 2\vert x$ or $\exists k \in \mathbb{Z},\ x = 2k+1$

Proof by Contradiction

Consider a statement

\[\forall x \in D \quad p(x) \implies q(x)\]

Assume that the statement is not true, i.e. $\neg ( p \implies q) = p \land \neg q$. Then show that this is impossible.

For example: prove $\forall a \in \mathbb{Z}$ and $\forall b \in \mathbb{Z}$ then

\[\text{$a$ is even } \land \text{ $b$ is even } \implies (a+b) \text{ is even}\]

by contradiction.

Proof: assume that $p \land \neg q$

1. this means we assume the following is true

   \[(\text{$a$ is even } \land \text{ $b$ is even }) \land \neg(a+b \text{ is even})\]

   notice this $\land$ induced by contradiction proof. This effectively allows us to use both LHS and RHS of the equation

2. this means

   \[(\text{$a$ is even } \land \text{ $b$ is even }) \land (a+b \text{ is odd})\]

3. this implies

   \[\exists k \in \mathbb{Z},\quad a=2k\\ \exists z \in \mathbb{Z},\quad b=2z\]

4. but this means

   \[a+b = 2(k+z)\quad \text{is even}\]

5. yet we claimed $(a+b)$ is not even. Is a contradiction.

Proof by Contrapositive

Given the statement

\[\forall x \in D \quad p(x) \implies q(x)\]

Prove by showing that $\forall x \quad \neg q(x) \implies \neg p(x)$, which might be easier in times.

• i.e. start with $\neg q(x)$, and conclude that $\neg p(x)$. e.g. by using a direct proof.
• this is useful usually when you realize the LHS of the original statement, i.e. $p(x)$ is hard to move forward

For Example: prove that $\forall r \in \mathbb{R}$, if $r$ is irrational, then $\sqrt{r}$ is also irrational.

• since this means $r \neq a/b$, which is hard to move forward. Hence we consider converting proof by contrapositive.

Proof: by contrapositive, then $\sqrt{r}$ is rational $\implies$ $r$ is rational. Using a direct proof

1. since $\sqrt{r} \in \Q$, this means

   \[\exists a,b \in \mathbb{Z}, \quad \sqrt{r}=\frac{a}{b}\]

2. then this means

   \[r = \frac{a^2}{b^2}\]

3. this means

   \[\exists c,d \in \Z, \quad r = \frac{c}{d}\]

   for example by letting $a^2=c$, $b^2=d$

4. this means $r \in \Q$.

For Example: let $a,b \in \Z$ prove that $a+b > 100 \implies ((a > 50) \lor (b > 50))$

Proof: We realize it is hard to move forward from $a+b > 100$ as we have two numbers on LHS. Consider using the contrapositive

\[((a \le 50) \land (b \le 50)) \implies a+b \le 100\]

the rest is obvious by direct proof.

Proof of IFF

Consider the statement

\[\forall x \in D\quad p(x) \iff q(x)\]

Then essentially you need to

• proof by any method that $p(x) \to q(x)$
• proof by any method that $q(x) \to p(x)$

For Example: prove that $\text{$x^2$is even} \iff \text{$x$is even}$. To prove this we need to prove both ways

Proof. We can first prove the forward direction

\[\text{$x$ is even}\implies\text{$x^2$ is even}\]

1. since $x$ is even, then $x=2a$ for some $a \in \Z$
2. therefore $x^2 = 4a^2$
3. hence $x^2 = 2 (2a^2)$
4. hence $x^2 = 2c$ for some $c \in \Z$
5. so $x^2$ is even

Now, we prove that

\[\text{$x^2$ is even}\implies\text{$x$ is even}\]

1. its hard to do a direct proof, we can try instead contrapositive

   \[\text{$x$ is odd}\implies\text{$x^2$ is odd}\]

2. then this means $x = 2a+1$ for some $a \in \Z$

3. hence $x^2 = 4a^2 + 2a + 1$

4. hence $x^2 = 2(2a^2 + a) + 1$

5. meaning $x^2 = 2c + 1$ for some $c \in \Z$

6. so $x^2$ is odd

Proof by Contradiction

In a proof by contradiction, assume the opposite of what you are trying to prove. Then you make logical deductions until you arrive to a contradiction.

For Example: Prove by contradiction that there are no integer $x,y$ that satisfy $5x+25y = 1723$

Proof: This means to prove that

\[\forall x,y \in \Z \quad 5x + 25y \neq 1723\]

By contradiction, we can first assume that this is false. Hence this means the below is true by assumption.

\[\exists x,y \in \Z \quad 5x + 25y =1723\]

1. let this be true. Then this means

   \[5(x+5y) = 1723\]

2. hence

   \[x + 5y = \frac{1723}{5}\]

3. hence contradiction as LHS is integer, but RHS is not.

Proof by Cases

In proof by cases, try to break the proof into cases, if your starting point is too general. Make sure that your cases span all possibilities

So the general format would be to prove

\[p_1 \lor \dots \lor p_n \implies q\]

by proving for each $p_i \implies q$ by proposition logic.

---

For Example: Profe that for any integer $x$, $x^2 + x$ is even.

Proof : this means that

\[\forall x \in \Z\quad \text{$x^2+x$ is even} \equiv \forall x \in \Z\quad (x\in \Z \implies \text{$x^2+x$ is even} )\]

this is straightforward using a direct proof, and essentially showing that $x(x+1)$ must include both an even number and an odd number.

To prove by cases, we can consider (inspired from the direct proof) that

\[\forall x \in \Z\quad (\text{$x$ is even} \lor \text{$x$ is odd} \implies \text{$x^2+x$ is even} )\]

• case 1: $x$ is even, then $x = 2a$ for some $a \in \Z$
  • then $x^2 + x = 2(2a^2 + a)$ is even.
• case 2: $x$ is odd, then $x=2a+1$
  • then $x^2 + x = 2(2a^2 + 3a + 1)$ is also even
• therefore, $x^2 + x$ is even.

Proof by Counter Example

Used to disprove some proposition, by finding an example such that the proposition is false.

Usually you will disprove

\[p \to q\]

meaning to find an example such that $p$ is true but $q$ is false.

Some “tricks/hints” when you are stuck:

1. keep in mind of your domain
2. try to create edge examples
3. try to prove it (though you know it will not hold), so you can look for pattern when this will likely fail

---

For example: disprove that $\forall a,b \in \Z\quad (a\vert b \land b\vert a)\implies a=b$

Proof: counter example: $a=-b$, e.g. $a=2$ and $b=-2$. Then LHS is true, but RHS is false.

You can see how this edge case come about if you attempted a direct proof to “attempt to” show this is true

1. let $a\vert b \land b\vert a$ is true
2. Then this means $a = xb$ and $b = ya$ for $x,y \in \Z$
3. hence this means $a = xy \cdot a$ hence $xy = 1$
4. but this means either $x = y = 1$ or $x=y=-1$.
5. in the latter case, this implies $a=-b$, which means LHS is true but RHS is false

Note that this is different from proof by contradiction, from which it is a) used to prove instead of disprove; b) flipped the entire proposition

Sets

In general, we we refer to sets, we consider unordered sets

We will distinguish between two types of collections: unordered sets (in which, order does not matter) and ordered sets or lists (in which order matters).

Unordered Sets

(Unordered) Set: is a collection of distinct object in which order does not matter.

for example:

\[p = \{ \text{eraser, pen, highlighter} \}\]

or you can also have an infinite set

\[\mathbb{Z} = \{ \dots, -2,-1,0,1,2,\dots \}\]

for us, in general we assume that counting numbers start with $1$

\[\mathbb{N} = \{ 1,2,3,\dots \}\]

though there are also some people considers $\mathbb{N}$ includes $0$. You can even have sets inside a set

\[bp = \{ \text{notebook, laptop, } \{ \text{eraser, pen, highlighter} \} \}\]

but if we the following is not a set

\[S = \{ 1,1,2,3 \}\]

since you have duplicates. This becomes a multiset, which we will not cover in this class.

Notation:

• belongs to $\in$. Means is a member/element in a set is denoted as

  \[a \in \mathbb{Z}\]

• empty set is denoted as either

  \[b = \{\},\quad\text{or}\quad b = \emptyset\]

• does not belong to $\notin$:

  \[\text{fridge} \notin \text{backpack}\]

  where backpack is a set.

some caution include that, let

\[bp = \{ \text{notebook, laptop, } \{ \text{eraser, pen, highlighter} \} \}\]

then technically

• $\text{notebook} \in bp$
• $\text{pen} \notin bp$ because “pen” is technically not a member of the set, but ${ \text{eraser, pen, highlighter} } \in bp$

Subset: let $A,B$ be two sets. $A$ is a subset of $B$ provided that every element in $A$ is also an element in $B$. We denote that

\[A \subseteq B\]

where this is “subset or equal”.

Note that the difference between $\in$ and $\subseteq$ is that

• $\in$ can be used with an element or set, since a set can be an element
• $\subseteq$ must only be used with a set

But note that we can translate the definition of subset to FOL:

Let $A,B$ be sets. Then

\[A \subseteq B \iff (\forall a \in A\quad a \in B)\]

(just as a practice) What if the domain is $\Z$, i.e. for both sets?

\[A \subseteq B \iff (\forall a \in \Z \quad a \in A \implies a \in B)\]

For Example:

• ${4} \subseteq { 1,2,3,4 }$ is true
• ${4} \nsubseteq { 1,2,3,{4} }$ since the element in LHS is $4$, whereas the element on RHS is ${4}$.
• ${{4}} \subseteq { 1,2,3,{4} }$ is true
• ${} \subseteq { 1,2,3,{4} }$ in fact, ${} \subseteq S$ for any set $S$.
• ${} \notin { 1,2,3,{4} }$ as empty set is not a member of the RHS.

Equality between sets: two sets are equal $A = B$ provided

\[A = B \iff A \subseteq B \land B \subseteq A\]

or we can write as FOL

\[A = B \iff (\forall a \quad a \in A \iff a \in B)\]

note that the above strictly says “take any element $a$ in the universe, if $a \in A$ then $a \in B$ and vice versa”. Therefore the below is wrong

\[A = B \iff (\forall a \quad a \in A \land a \in B)\]

this instead says “every element in the universe is both in $A$ and $B$”. But yuo can do something like (correct)

\[A = B \iff (\forall a \in A \quad a \in B) \land (\forall a \in B \quad a \in A)\]

which is basically saying $A \subseteq B \land B \subseteq A$.

Proper Subset: being a subset but not equal

\[A \subset B \iff A \subseteq B \land A \neq B\]

For Example: $\Z \subset \Q$ because

\[\Z \subset \Q \iff \Z \subseteq \Q \land \Z \neq \Q\]

and of course

• ${1} \subset {1,2}$
• ${1} \subseteq {1,2}$
• but ${1,2} \subseteq {1,2}$ only

Universal Set denoted as $U$, which is the set of everything under consideration.

(Barber’/Russell’s paradox: in general, whenever there is self-reference, there is typically a paradox)

Power Set: the set of all subsets of a set $A$ is called a power set $P(A)$

For example, let $S = {1,2}$, then

\[P(S) = \{ \empty, \{1\}, \{2\}, \{1,2\} \}\]

basically, a set including $0$ elements on the set, $1$ element of the set, and then $2$ elements of the set.

This means empty set is an element of any powerset, so that

\[P(\empty) = \{ \empty \}\]

How many elements are there in a powerset? There are $2^k$ elements in the powerset $P(S)$, for $k$ is the number of elements in $S$.

• proof 1: For each element in $P(S)$, e.g. let $S={a,b,c}$, then any power set is essentially:

  	a	b	c
  $\empty$	F	F	F
  ${a}$	T	F	F
  ${b}$	F	T	F
  ${c}$	F	F	T
  ${a,b}$	T	T	F
  …

  so basically it is the number of combinations of the truth table

• proof 2: just use

  \[{0 \choose k} + {1 \choose k} + \cdots + {k \choose k} =2^k\]

Finite Set: a finite set is a set has $n$ elements for $n \in \Z^+$. Otherwise we call the set infinite.

Cardinality: let $A$ be a finite set, the number of elements in $A$ is called cardinality, denoted as $\vert A\vert$

For example:

• if $A$ has $n$ elements, then $\vert A\vert =n$.
• $S={1,2,3,…,20}$. Then $\vert S\vert =20$, and that $\vert P(S)\vert = 2^{20}$.
• $\vert \Z\vert$ is then technically sloppy notation as $\Z$ is not a finite set, but we will use this later in functions.

We have seen a lot of connections between FOL and sets. We will see how to build set using “set builders”, a compact way to define your set using FOL (and PL):

\[S = \{ x | P(x) \}\]

where $P(x)$ is a FOL

For Example:

• instead of $S={1,2,3…,100}$, you can write

  \[S = \{ x | x \in \Z \land (1 \le x \le 100) \}\]

  to avoid any ambiguity

• the set of even integers is then

  \[E = \{ x | x\in \Z \land 2|x \}\]

  or more properly

  \[E = \{ x | x\in \Z \land (\exists a \in \Z \quad x=2a) \}\]

• define the set of composite (non prime) number (excluding 1)

  \[S = \{ x | x\in \Z^+ \land \underbrace{(\exists a \in \Z^+ \quad (1<a<x) \land a|x)}_{\text{$a$ is non-prime}} \}\]

  which basically says “every member in the set is (a positive integer AND is non-prime)”.

  note that it would be “incorrect” to write

  \[S = \{ x | x\in \Z^+ \quad {(\exists a \in \Z^+ \quad (1<a<x) \land a|x)}\}\]

  because we are not talking about $\forall x \in \Z^+$ or $\exists x \in \Z^+$, we are just letting $x\in \Z^+$ being a property of elements in this set.

• define $S={1,4,9,16,…,100}$ by set builder:

  \[S=\{x|x\in Z\land (1\le x \le 100) \land (\exists a\in \Z \quad x=a^2 )\}\]

  or you can

  \[S=\{x|x\in Z\land (1\le x \le 100) \land (\sqrt{x} \in \Z) \}\]

  technically you can even omit $x\in \Z$ since by closure property this is implied by $\sqrt{x} \in \Z$.

Make sure that your set builder includes all the elements and only the elements intended, i.e. is correct and complete. This mean you should check

\[\forall x \quad (x \in S \iff P(x))\]

so that forward is correctness, and backward is completeness (i.e. $\forall x \in U \quad P(x) \to x\in S$)

Set Operations and Properties

Set operations defined between 2 sets

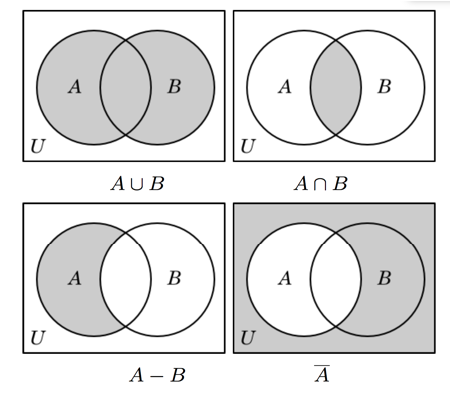
• intersection of two sets:

  \[A \cap B = \{x | (x\in A) \land (x \in B) \}\]

  basically conjunction in PL

• union of two sets

  \[A \cup B = \{x | (x\in A) \lor (x \in B) \}\]

• difference between two sets

  \[A - B = \{x | (x\in A) \land (x \neq B) \}\]

  in $A$ but no in $B$

• complement (with respect to the universe)

  \[A^c = \bar{A} = \{x | x \notin A\}\]

  where $x \in U$ part of the universe is assumed.

• Cartesian product between two sets

  \[A\times B = \{ (a,b) | a\in A\land b \in B \}\]

  for example $A={ c,d }$ and $B={e,f,g}$, then $A\times B={ (c,e),(c,f),(c,g),(d,e), (d,f),(d,g) }$. Therefore, this also means that the cardinality $\vert A \times B\vert = \vert A\vert \cdot \vert B\vert$.

or even Venn Diagram

Then of course, you also have certain properties of those operations

For Example:: prove that $\overline{A \cap B} = \bar{A} \cup \bar{B}$ using set builders

since by definition of set operations

\[\overline{A \cap B} = \{ x | x \notin (A \cap B) \}\]

then we can rewrite as

\[\overline{A \cap B} = \{ x | \neg (x \in (A \cap B)) \}\]

but we can then define $A \cap B$ by

\[\overline{A \cap B} = \{ x | \neg (x \in A \land x \in B) \}\]

then by De Morgan

\[\overline{A \cap B} = \{ x | x \notin A \lor x\notin B \}\]

then finally just put it into our target form

\[\overline{A \cap B} = \{ x | x \in \bar{A} \lor x \in \bar{B} \}\]

hence

\[\overline{A \cap B} = \{ x | x \in \bar{A} \cup \bar{B} \}\]

But in general, there will be multiple ways to prove this.

Proofs on Sets

We have covered a bit of how to prove set equality in previous section in an example. Here we discuss more techniques that you can use for set proofs.

1. To prove that $A \subseteq B$
   • let $x \in A$
   • …
   • therefore $x \in B$
2. To prove $A = B$ by showing that $A \subseteq B \land B \subseteq A$
   • show that $A \subseteq B$ by showing $x \in A$ … therefore $x \in B$
   • show that $B \subseteq A$ by showing $x \in B$ … therefore $x \in A$

To prove equality, you can use any of the three methods

1. (element level) use set builder
   • e.g. see previous section on proving $\overline{A \cap B} = \bar{A} \cup \bar{B}$
2. (element level) use the subset technique above, e.g. to prove $F=E$
   • i.e. you can either prove $x\in F \implies x\in E$, and then again for $x \in E \implies x\in F$
   • or you can shorten the above and show that $x\in F \iff x \in E$ (e.g. see the last example in Relations)
3. (set level) using set operations, e.g. distributivity, De Morgan, etc.

For Example: let $F$ and $E$ be two sets.

\[F = \{z|z \in \Z \land z = a+b \land a\text{ is odd} \land b \text{ is odd}\}\] \[E = \{ x | x \in \Z \land 2 |x \}\]

Prove that $F=E$.

• Prove that $F \subseteq E$

  1. let $x \in F$.

  2. Then this means $x = a + b$ for some $a,b\in \Z$ where $a,b$ is odd

  3. therefore this means

     \[x = (2t+1)+(2w+1)\]

  4. we can rewrite this as

     \[x = 2(t+w+1)\]

  5. so $x$ is even, and $2\vert x$

  6. therefore $x \in E$

• Prove that $E \subseteq F$

  1. let $x \in E$

  2. then this means $x=2t$ for some $t \in \Z$

  3. then we can rewrite this as

     \[x = (2t+1) - 1\]

  4. therefore we can have $a = 2t+1$ and $b=-1$, meaning $a,b$ are odd

  5. therefore $x \in F$

Size of the Union

Size of the union: Let $A,B$ be two sets. Then

\[|A\cup B| = |A| + |B| - |A \cap B|\]

But if $A,B$ are disjoint, then

\[|A \cup B| = |A| + |B|\]

For example: What is $\vert A \cup B\cup C\vert$

Following the step above, we have

\[\begin{align*} &\quad |A \cup B \cup C| \\ &= |A \cup B| + |C| - |A \cup B \cap C| \\ &= |A|+|B|-|A \cap B| + |C| - |(A \cup B) \cap C| \end{align*}\]

but notice that:

\[(A \cup B) \cap C = (A\cap C) \cup (B \cap C)\]

Hence

\[|(A \cup B) \cap C| = |A\cap C| + |B \cap C| - |A \cap B \cap C|\]

Hence we obtain

\[|A \cup B \cup C| = |A|+|B|+|C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|\]

Note that this including and then excluding back will also be touched on in counting, called the Principle of Inclusion Exclusion.

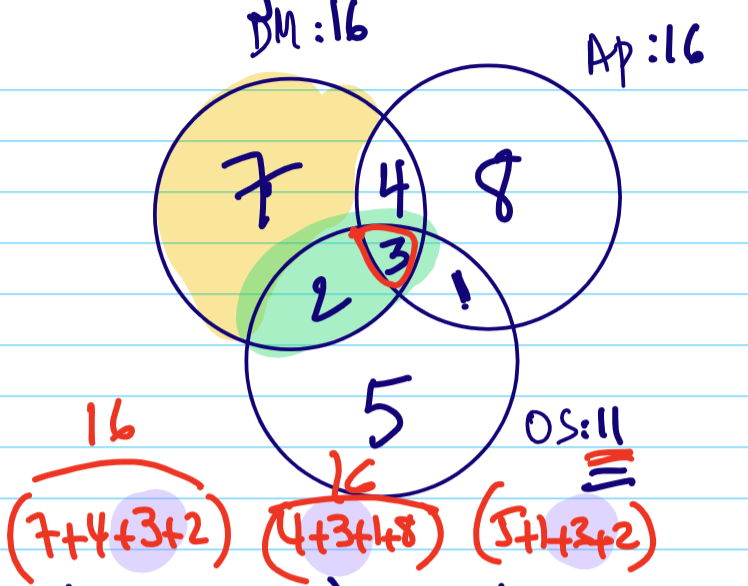
Another in class example: Let there be 16 people taking DM, 16 taking AP, and 11 taking OS. We are also given that

• 5 taking both DM and OS, and among them 3 taking AP as well
• 8 people taking AP only
• 5 people taking OS only

We want to know how many want to take DM only.

Here, we solve it using Venn Diagram

Ordered Sets/Lists

Now, we turn to ordered sets, where the order of the elements matter.

A list is an ordered set of element, and elements can now repeat. This is often denoted using parenthesis

\[(e_1,e_2, \dots, e_n)\]

For example:

• $(9,1,1)$ is a valid ordered list

• we actually touched on this before

  \[A\times B = \{ \underbrace{(a,b)}_{\text{a list}} | a\in A\land b \in B \}\]

  where order mattered, so that $A \times B \neq B \times A$.

• binary representation of numbers are also lists, so that all of the below are different lists: $101,110,011$.

Relations

Remember that for Cartesian product, we had

\[A\times B = \{ (a,b) | a\in A\land b \in B \}\]

so that let $S={A,D }$ being Annie and Daniel, and $C={DM, OS}$ being Discret Math and OS. Then

\[S \times C = \{ (A,DM),(A,OS),(D,DM),(D,OS) \}\]

but this doesn’t mean anything. Say we want to use this to represent “taking classes”

So we are taking subset to represent a meaningful relationship. i.e.

\[R_{\mathrm{take class}} = \{ (A,DM),(D,DM) \}\]

hence also $R_{\mathrm{take class}} \subseteq (S \times C)$

Relation: let $A,B$ be two sets. We say that $R$ is a relation from $A$ to $B$ provided

\[R \subseteq A \times B\]

and that $R$ is a set of pairs.

For Example:

• Let $A = {1,2}$. Then

  \[A \times A = \{ (1,1),(1,2),(2,1),(2,2) \}\]

  consider a relation

  \[R = \{ (1,1),(1,2),(2,2) \}\]

  then this $R$ means $\le$. in other words:

  \[(x,y)\in R \iff x<y\]

• Let $A = {1,2}$. Let $R_{even}$ be defined from $A$ to $A$

  \[(x,y) \in R_{even} \iff x+y \text{ is even}\]

  then this means

  \[R_{even} = \{ (1,1),(2,2) \}\]

  or using set builders, this means

  \[R_{even} = \{ (x,y) | x\in A \land y \in A \land 2|(x+y) \}\]

In general, we notate the relation as two ways

\[(x,y) \in R_{even} \iff x+y \text{ is even}\]

or

\[x R_{even} y \iff x+y \text{ is even}\]

For Example: Let $R$ be a relation on $\Z$, i.e. from $\Z$ to $\Z$.

\[x R y \iff x \text{ divides }y\]

then what is $R$? We can first list a few examples

\[R = \{ (2,4),(2,6),(1,2), \dots \}\]

meaning

\[R = \{ (x,y) | x\in \Z \land y \in \Z \land x|y \}\]

Note that a relation can involve two or more sets, i.e. n-ary relations.

For Example: a simple one

\[R = \{ (a,b,c)| a \in A \land b \in B \land c \in C \}\]

is a legit relation.

Inverse of a Relation: let $R$ be a relation from $A$ to $B$. We define the inverse of $R$ denoted as $R^{-1}$ as follows

\[\forall x \in A,\forall y\in B\qquad (x,y)\in R \iff (y,x) \in R^{-1}\]

so that $R^{-1}$ is a relation from $B$ to $A$.

Proposition: inverse of inverse is itself

\[R = (R^1)^{-1}\]

Proof (using the subset technique):

• prove $R \subseteq (R^{-1})^{-1}$:
  1. let $(x,y) \in R$.
  2. then by definition of inverse $(y,x) \in R^{-1}$
  3. therefore $(x,y) \in (R^{-1})^{-1}$
• prove $(R^{-1})^{-1} \subseteq R$:
  1. let $(x,y) \in (R^{-1})^{-1}$.
  2. then by definition of inverse $(y,x) \in R^{-1}$
  3. therefore $(x,y) \in R$

But we notice that the step is symmetrical/same in both ways. Hence this proof can be proven in much fewer lines

\[(x,y) \in R \iff (y,x) \in R^{-1} \iff (x,y) \in (R^{-1})^{-1}\]

Representation of Relation

We can visualize a relation using:

1. Directed Graphs (DiGraphs)
2. Matrix (a boolean matrix)

Digraph: a visual representation of a relation with a set of nodes (vertices) connected by directed edges (arcs)

For example: this relation is a subset of cross product $R \subseteq {1,2,3}\times {1,2,3}$

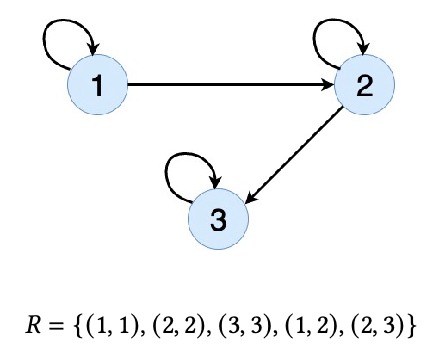
notice that here each node is an element in the pair, and in general, the graph does not have to be connected (e.g. imagine $R={(1,1),(2,2)}$)

Matrix: A relation $𝑅$ defined from set $𝐴$ to set $𝐵$ can be represented by a Boolean matrix in which the rows are elements of $𝐴$ and the columns are represented elements of $𝐵$ and each entry of the matrix at row $𝑖$ column $𝑗$ is 1 if there is a relation through $𝑅$ between the ith element in $𝐴$ and the jth element in $𝐵$, otherwise the entry is zero.

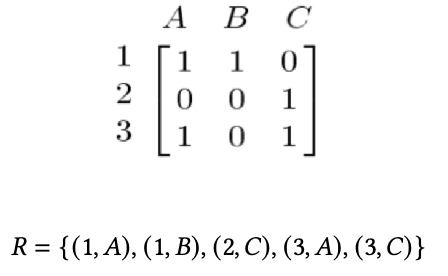
Note that since essentially relations are sets:

All the properties on set operations apply to relations as well. For instance, intersection is commutative for relations, and we have $R_1 \cap R_2 = R_2 \cap R_1$

Properties of Relations

Some relations can have special properties, which would come useful later

• Reflexivity: let $R$ be a relation defined on a set $A$. The relation is reflexive

  \[R\text{ is reflexive}\iff \forall x \in A\quad (x,x)\in R\]

  or you can also denote

  \[R\text{ is reflexive}\iff \forall x \in A\quad xRx\]

  note that

  • graphically, it means for $\forall x\in A$, you have a self-loop

  • the following would be incorrect: $R^{-1} = R$. e.g. let $R={(1,2),(2,1)}$

• Not Reflexivity: then there exists a pair that is not in $R$:

  \[R\text{ is not reflexive}\iff \exists x \in A\quad (x,x)\notin R\]

  or you can also denote

  \[R\text{ is not reflexive}\iff \exists x \in A\quad x\not R x\]

• Irreflexive: then basically no self-loops:

  \[R\text{ is irreflexive}\iff \forall x \in A\quad (x,x)\notin R\]

  examples include “is parent of”, “>”.

• Symmetric: “all directed edges = undirected edges”

  \[R\text{ is symmetric}\iff \forall x,y \in A\quad (x,y)\in R \implies (y,x)\in R\]

  e.g. $A={1,2,3}$, and a symmetric relation $R={(1,2),(2,1)}$

• Not symmetric: negation of the above. There exist a pair that is not “reciprocal” (including “self-reciprocity”)

  \[R\text{ is not symmetric}\iff \exists x,y \in A\quad (x,y)\in R \land (y,x)\notin R\]

• Antisymmetric: there is never reciprocity (except “self-reciprocity”)

  \[R\text{ is anti-symmetric}\iff \forall x,y \in A\quad xRy \land yRx \implies x=y\]

  note that the this is different from the below

  \[R\text{ is anti-symmetric}\iff \forall x,y \in A\quad (x,y)\in R \implies (y,x)\notin R\]

  the upshot is that you can have a relation that is both symmetric and anti-symmetric, and also being both symmetric and not anti-sym.

• Transitivity: very useful later

  \[R\text{ is transitive}\iff \forall x,y,z \in A\quad xRy \land yRz \implies xRz\]

Note that when you have $\forall x\in A \quad \text{blablabla}$, be careful how $A$ is defined

For Example: Consider the following relations defined by $A = {1,2,3}$

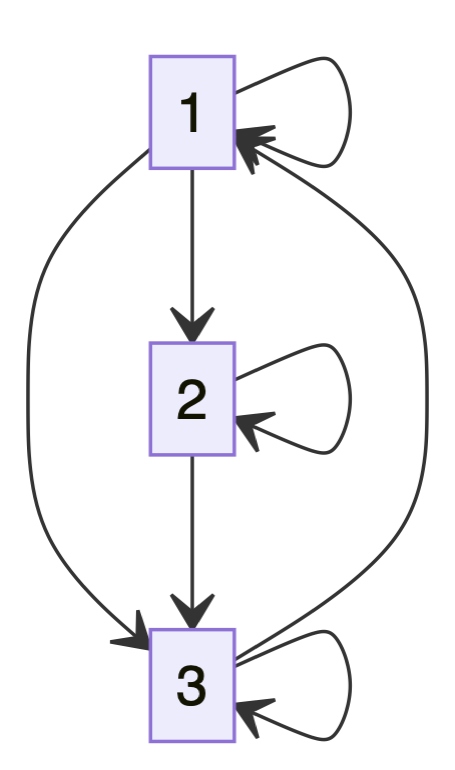
• $R_1= { (1,3),(3,3),(3,1),(2,2),(2,3),(1,1),(1,2) }$

  • is reflexive: because $\forall x \in {1,2,3}\quad xRx$
  • not symmetric: because $(2,3)\in R \land (3,2) \notin R$
  • not anti-symmetric: because $1R3\land 3R1$ but $1\neq 3$
  • not transitive: $2R3\land 3R1$ but $2 \not R1$ (better see this drawing a Digram)

  

• $R_2 = { (1,1),(2,2),(3,3) }$ is symmetric and anti-symmetric

  • is reflexive
  • is symmetric: because for each element in the relation, $xRy \to yRx$
  • is anti-symmetric: yes. Just proof by enumeration.
  • is transitive: yes. Just proof by enumeration.

• $R_3={ (1,1),(1,2),(2,3),(3,1),(1,3) }$

  • not irreflexive: because $(1,1)$ is there
  • is symmetric: no
  • is anti-symmetric: no, because $(1,3)$ and $(3,1)$ exists
  • is transitive: no, because $(2,3)$ and $(3,1)$ but no $(2,1)$

• $R_4 = { (1,2),(2,3),(1,3) }$

  • is irreflexive: no self-loops
  • is anti-symmetric: yes, because there is no reciprocity whatsoever
  • is transitive: yes, proof by enumeration

Consider the following $R$ acting on $\Z$:

$R$	reflexive	irreflexive	symmetric	anti-symmetric	transitive
$=$	yes	no	yes	yes	yes
$\le$	yes	no	no	yes	yes
$<$	no	yes	no	yes	yes

where:

• $R_=$ is symmetric because if $x=y \implies y=x$, and is transitive, since $x=y\land y=z \implies x=z$. Finally it is also anti-symmetric because $a=b\land b =a \implies a=b$ (different from transitive)
• $R_\le$ is reflexive since $\forall x\in \Z\quad x\le x$. Hence this is also not irreflexive. It is also not symmetric since $1 \le 2$ but $2 \not \le 1$. By axioms $a \le b \land b \le a\implies a=b$ is anti-symmetric.
• $R_<$ is anti-symmetric because of benefit of doubt: $a < b \land b < a\implies a=b$ is true because LHS is always false.

Equivalence Relation: Let $R$ be a relation on $A$. We call a relation an equivalence relation provided

1. $R$ is reflexive
2. $R$ is symmetric
3. $R$ is transitive

For example, let $R$ be a relation between sets “$R$: have same cardinality”. So that (notice now we are operating on sets) let $A,B$ be sets:

\[A,B\subseteq S\quad ARB\iff |A| = |B|\]

note that since we are operating on sets being subsets of $S$, this means our relations are $R\subseteq P(S)\times P(S)$ defined on power sets.

Then, we want to prove that $R$ is an equivalence relation:

• is reflexive, since $\forall A \subseteq S\quad \vert A\vert =\vert A\vert$
• is symmetric, since $\forall A,B\subseteq S \quad \vert A\vert =\vert B\vert \implies \vert B\vert =\vert A\vert$
• is transitive, since $\forall A,B \subseteq S\quad \vert A\vert =\vert B\vert \land \vert B\vert =\vert C\vert \implies \vert A\vert =\vert C\vert$

Why do we care about this property? Because

Equivalence Classes: let $R$ be an equivalence relation on $A$. Then let $a\in A$. The equivalence class of $a$, denoted as $[a]$ is the set of all elements in $A$, related to $a$ through the relation $R$:

\[[a] = \{ x | x\in A \land x Ra \}\]

notice that it is defined through a particular relation, and you will see $a$ itself will always belong to this set

Why do we care about equivalence sets? You will see that

• objects in an equivalence sets share similar properties

• can partitions sets into equivalence classes - cutting down the amount of cases necessary to prove something.

For example:

• let $R$ being the cardinality of sets. Then $[\empty] = {\empty}$
• let $R$ be the relation “Have same parents as you” $[\text{you}] = {\text{you, your siblings}}$

Properties of Equivalence Classes: let $R$ be an equivalence class on $A$, then

1. $a\in [a]$ is always there (because an equivalence class is reflexive)
2. $\forall a \in A\quad [a]\neq \empty$ due to the above
3. if I take the equivalence class of all elements, then $\bigcup_{a\in A}[a] = A$

Proof for $\bigcup_{a\in A}[a] = A$. We notice that this is basically proving equality between sets. We can then do:

• $\bigcup_{a\in A}[a] \subseteq A$:
  1. let $x \in \bigcup_{a\in A}[a]$.
  2. then this means $x$ must belong to some equivalence class $\exists a\in A\quad x\in [a]$
  3. but we know $[a]\subseteq A$
  4. therefore $x \in A$
• $A \subseteq \bigcup_{a\in A}[a]$
  1. let $x\in A$
  2. then $x\in [x]$
  3. therefore $x \in \bigcup_{a\in A}[a]$.

For example, consider $R$ be defined on a set of 2x2 board configuration $S$, so that:

\[\text{board}_1\ R\ \text{board}_2 \iff \text{board 1 and board 2 can be obtained form each other by reflection or rotation}\]

we can:

1. show that this relation is an equivalence relation (i.e. is reflexive, symmetric, and transitive)

2. we can find all its equivalence classes and realize they are partitions!

   

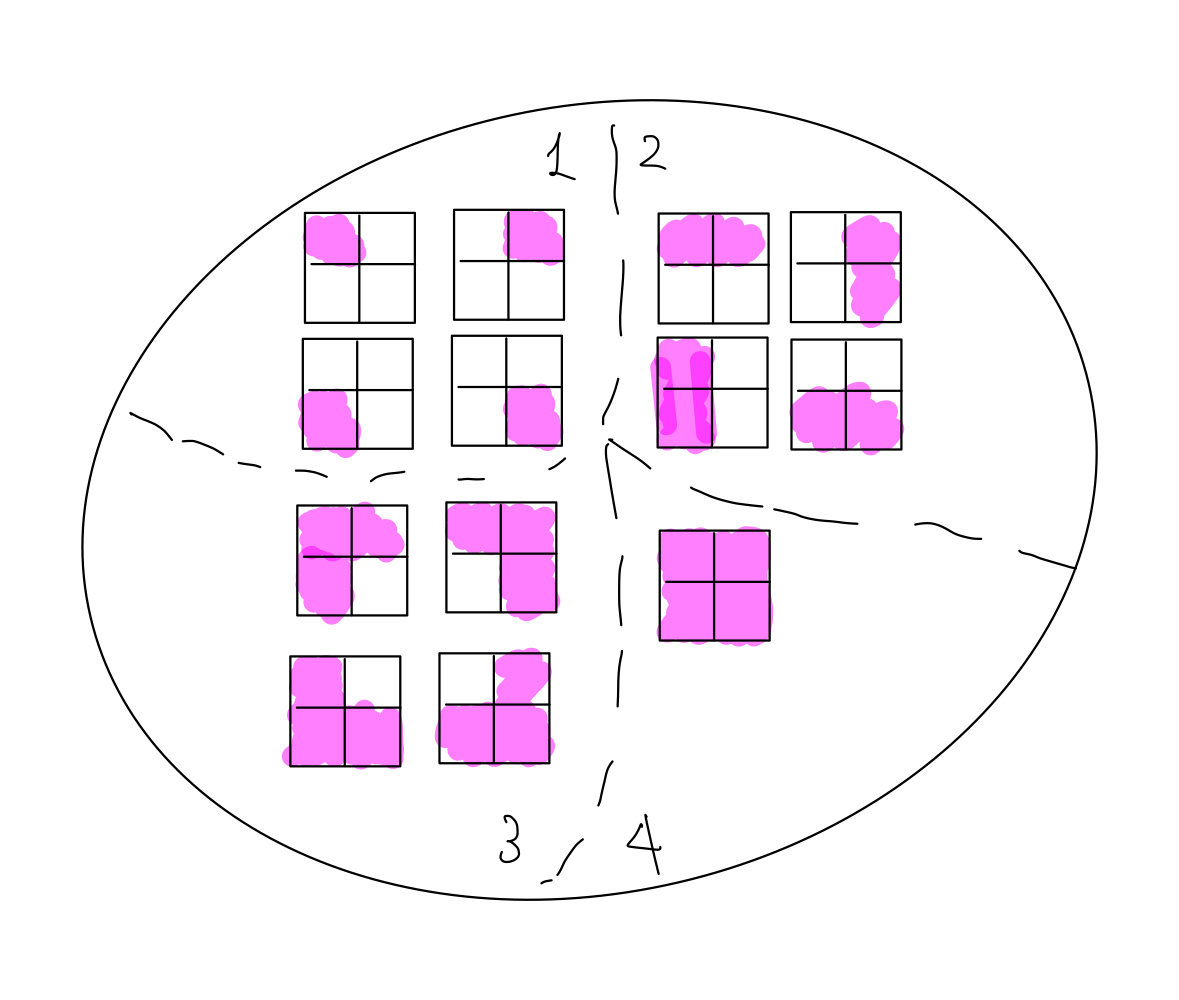
Relation of congruence modulo n

This is used a lot in cryptography, and number theory.

Congruence modulo n: let $n$ be a positive integer. We say that two integers $x,y\in \Z$ are congruent modulo n:

\[x \equiv y(\mathrm{mod}\ n)\]

provided that $n$ divides the difference $n\vert (x-y)$. Note that In the context of relations, ”$\equiv$” means congruent.

For example,

• $3\equiv 13 (\mathrm{mod}\ 10)$ reads as “$3$ is congruent to $13$ modulo $10$”
• $13\equiv 3 (\mathrm{mod}\ 10)$
• $3\not\equiv 22 (\mathrm{mod}\ 10)$

Theorem: let $n$ be a positive integer. The relation “congruent modulo $n$” is an equivalence relation on the set of integers

Proof:

• is reflexive. This means we want to show that

  \[\forall x \in \Z,\quad x\equiv x(\mathrm{mod}\ n)\]

  by definition, this means $\iff$ $n\vert (x-x)$, which is true since $n\vert 0$.

• is symmetric. This means we want to show that

  \[\forall x,y \in \Z,\quad x\equiv y(\mathrm{mod}\ n)\implies y\equiv x(\mathrm{mod}\ n)\]

  then

  1. let $x\equiv y(\mathrm{mod}\ x)$. This means $n\vert (x-y)$
  2. so $n\vert -(x-y)$
  3. hence $n\vert (y-x)$
  4. therefore $y\equiv x(\mathrm{mod}\ y)$

• is transitive. This means to prove that

  \[\forall x,y,z\in \Z,\quad x\equiv y(\mathrm{mod}\ n)\land y\equiv z(\mathrm{mod}\ n) \implies x\equiv z(\mathrm{mod}\ n)\]

  then

  

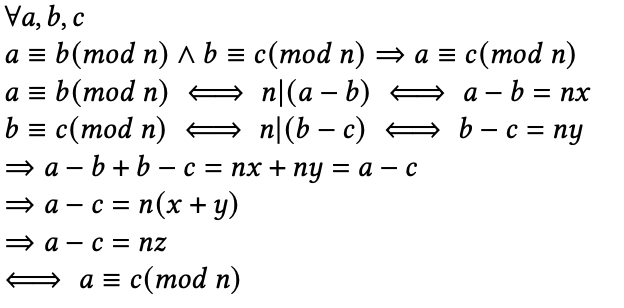
Partition: a partition of a set is a collection of non-empty pairwise-disjoint subset of $S$, so that the union gives $S$

For example ,consider the congruence modolo $2$ of $\Z$ is

\[\forall a,b\in \Z,\quad a \equiv b(\mathrm{mod}\ 2)\]

where basically $a \equiv b(\mathrm{mod}\ 2)$is $aRb$.

• then we have

  \[[0] = \{ x | x \in \Z \land 0 \equiv x \text{ (mod 2)} \} = \{ ..., -4,-2,0,2,4,... \}\]

• continuing

  \[[1] = \{ x | x \in \Z \land 1 \equiv x \text{ (mod 2)} \} = \{...-3,-1,1,3,... \}\]

• but eventually you will realize

  \[[2] = \{ x | x \in \Z \land 2 \equiv x \text{ (mod 2)} \} = \{ ..., -4,-2,0,2,4,... \}\]

  which is same as $[0]$!

• and you can show that also $[3] = [1]$.

As a result , this creates a partition of $\Z$ into two partitions, even and odd numbers (if you consider equivalences for $\mod 4$, you get 4 partitions, etc.)

Proposition: let $n \in \Z ^+$ and $a,b \in \Z$. Then

\[a \equiv b (\mathrm{mod}\ n) \iff a\ \mathrm{mod}\ n = b\ \mathrm{mod}\ n\]

which you can try to prove as an exercise.

• note that in general, proofs with relation are essentially set proofs. See HW6 Q6 or recitation 8 for example.

Functions

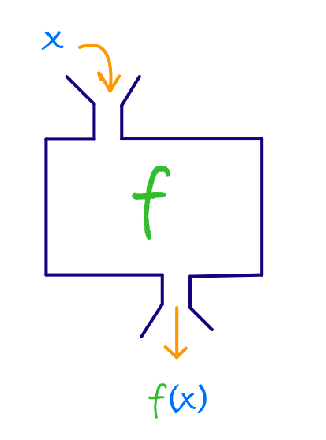
It can be seen also as a type of relation where you basically have ${(x,f(x))}$. For example, if $f(x)=x^2$, then on the set of integers:

\[f=\{(0,0),(1,1), (-1,1), (2,4), (-2,4),...\}\]

Functions: let $A,B$ be two sets. A function $f$ from $A$ to $B$ denoted

\[f:A \to B\]

so $f \subseteq A \times B$ where each element of $A$ appears exactly once as a first element of the ordered pairs of $f$. (i.e. vertical line test). So that

\[\text{$f$ is a function from $A$ to $B$}\iff \forall a \in A\quad \exists! b \in B \quad b = f(a)\]

i.e. there is only one $b$ for each $f(a)$.

Some terminology to be used here. Let $f:A \to B$. Then

• $A$ is called the domain
• $B$ is the co-domain
• $b\in B$ is called the image of $a$
• $a\in A$ is called the pre-image of $b$

More formally, the set of all second elements of the pairs of $f$ is called the image of $f$:

\[\mathrm{image}(f) = \{ b | b \in B \land \exists a \in A\land f(a)=b \}\]

so that $\mathrm{image}(f) \subseteq B$

For example: let $A = {1,2,3,4}$ and $B={1,2,3,4,7,10,12}$.

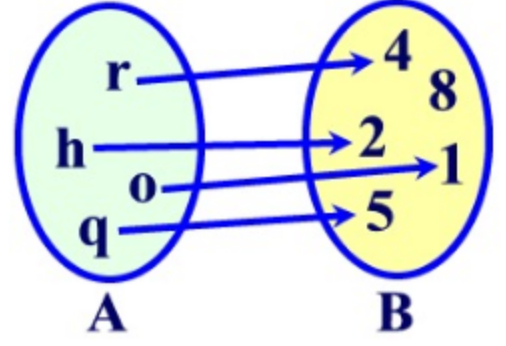
• let $f={(1,2),(2,3),(4,3),(3,1)}$. This is a valid function as each input $a\in A$ has a unique output.
  • the image of $f$ is then ${2,3,1}$.
• let $f={(1,2),(2,3),(4,3)}$. This is a not valid function as $a=3$ has undefined output.

---

One way to visualize functions is bipartite graph. For example the function

\[f=\{(1,2),(2,3),(4,3),(3,1)\}\]

can be visualized as

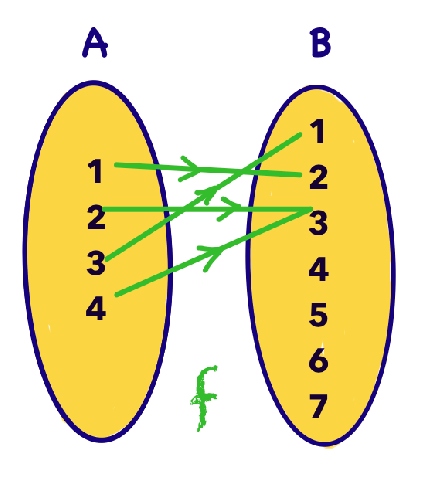
so that the “vertical line test” in discrete function is that each $a\in A$ has only one edge going out.

For example, let $f:{0,1}\times {0,1} \to \N \cup {0}$

• so that basically $A={(0,0),(0,1),(1,0),(1,1)}$, and $B={0,1,2,3,…}$

• and you are given:

  

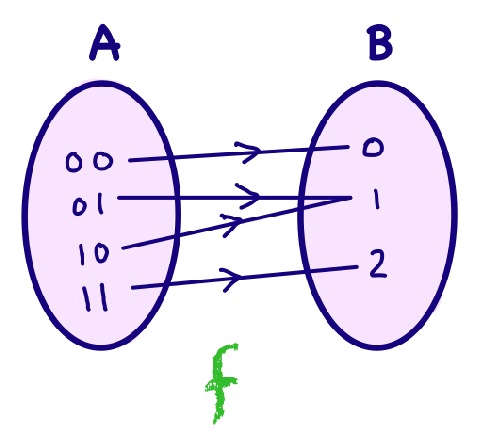
• is this a valid function? Yes, every $a\in A$ has a unique (only one) output.

• and also $\mathrm{image}(f)={0,1,2} \subseteq \N \cup {0}$.

Properties of Functions

Onto/surjective function: let $f:A \to B$ be a function. $f$ is onto IFF every element of $B$ has a pre-image. You can translate this into FOL

\[\forall b \in B \quad (\exists a \in A\quad b=f(a))\]

as a result, $\mathrm{image}(f)=B$. For example, $A={(0,0),(0,1),(1,0),(1,1)}$, $B={0,1,2}$:

so every element in $B$ receives at *least* one 1 pre-image.

• for example, $f(x)=x^2$ for $x \in \Z$ is not onto since $5 \in \Z$ but there is no integer with $x^2 = 5$
• and observe that $\text{$f$is onto\ }\implies \vert A\vert \ge \vert B\vert$
• is visually is also the pigeon hole principle ($A$ are the pigeons)

One-to-one/injection function: $f$ is one to one IFF no two elements of $A$ has the same image in $B$, i.e. every element in $B$ receives at *most* 1 pre-image. Note that this means one-to-one function does not have to be onto functions, i.e. you DON’T need $\mathrm{image}(f)=B$. Into FOL we have:

\[\forall a_1,a_2 \in A\quad a_1 \neq a_2 \implies f(a_1) \neq f(a_2)\]

or you can re-write this as contrapositive

\[\forall a_1,a_2 \in A\quad f(a_1) = f(a_2) \implies a_1 = a_2\]

which would be easier to use during proofs.

• for example, $f(x)=x^2$ for $x \in \Z$ is not one-to-one since you can have $4=(+2)^2 = (-2)^2$.
• and observe that $\text{$f$is one-to-one\ }\implies \vert A\vert \le \vert B\vert$

This means:

• to prove a function is onto: take an arbitrary element $b \in B$, show it has a pre-image in $A$
• to prove a function is one-to-one: take two arbitrary elements $a_1, a_2 \in A$, show that (e.g. direct proof) $f(a_1) = f(a_2) \implies a_1 = a_2$

For Example: let a function $f: \Q \to \Q$, and $f(x)=2x+1$.

• prove that $f$ is onto.
  • let $b \in \Q$ be an arbitrary element
  • then $b=2(x+1) \implies x = (b-1)/2$
  • but since $b\in \Q$, therefore $x \in \Q$
  • hence there is a pre-image $x\in \Q$ such that $f(x)=b$.
  • so $f$ is onto
• prove that $f$ is one-to-one
• let $a_1,a_2 \in \Q$ and that $f(a_1)=f(a_2)$
• then this $\implies 2a_1 + 1 = 2a_2 + 1$
• so $\implies a_1= a_2$
• therefore $f$ is one-to-one

Bijection: let $f:A \to B$ be a function that is both onto and one-to-one, then $f$ is a bijection, i.e. every element in $B$ receives exactly one pre-image

• and observe that $\text{$f$is a bijection\ }\implies \vert A\vert = \vert B\vert$

For Example: consider

• let $f_1 : \Z^+{odd} \to Z^+{even}$ and $f_1(x)=x+1$ is a bijection as it is both onto (each $b$ has a pre-image) and one-to-one (every $b$ has at most one). This implies, intuitively, that $\vert Z^+{odd}\vert = \vert Z^+{even}\vert$

• let $f_2 : \Z^+ \to Z^+{even}$ and $f_1(x)=2x$ is also bijection. But this unintuitively implies $\vert Z^+\vert = \vert Z^+{even}\vert$! in general for infinite sets, "cardinality" doesn't really exist.

Composition of Functions

Consider two functions:

• $f: A \to B$ and $g: C \to D$
• let $\mathrm{image}(f) \subseteq C$

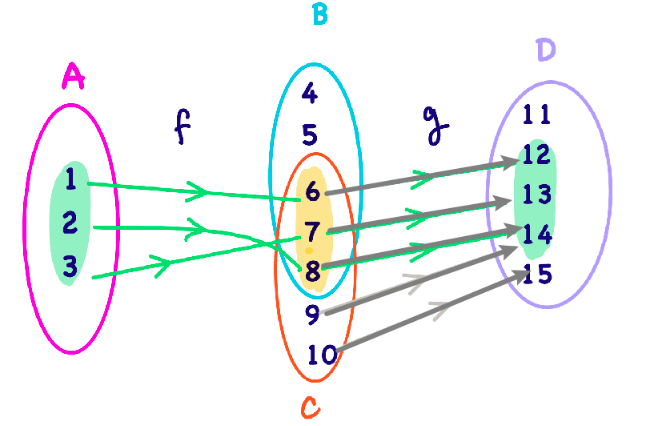
Composition: let $f: A \to B$ and $g: C \to D$, and $\mathrm{image}(f) \subseteq C$. The composition of functions $f$ and $g$ is defined as

\[g\circ f: A \to D,\quad g\circ f (x) = g(f(x))\]

note that we need $\mathrm{image}(f) \subseteq C$, not necessarily $B \subseteq C$.

For example: let $f:\Z \to \Z$ and $g : \Z \to \Z$

• let $f(x) = x^2+1$ and $g(x)=2x-3$. THen $g\circ f(x) = g(x^2+1) = 2(x^2+1)-3=2x^2-1$

Composition of Functions preserve the property of $f,g$ if they share the same property. If $f,g$ have different properties, it is more complicated.

• e.g. $f$ is many-to-one and $g$ is one-to-one then $f\circ g$ is many-to-one

Inverse of Functions

Identity Function: the identity function denoted $I_A$ is defined on $A$ to have:

\[I_A: A \to A,\quad I_A(a)=a\]

Inverse Function: let $f: A\to B$. If there exists a function $g: B \to A$ such that

\[g\circ f = I_A,\quad f\circ g = I_B\]

then $g$ is called the inverse of $f$, called $g=f^{-1}$.

• basically you want $f \circ f^{-1} = I_B$. and $f^{-1}\circ f = I_A$.

For Example

• let $f(x)=3x-2$. What is $f^{-1}$ Essentially we are finding $x$ from $y=f(x)$, therefore $f^{-1}(x)=(x+2)/3$

Note that inverse $f^{-1}$ might not exist, i.e. not a function. E.g. $f(x)={(1,a),(2,a)}$, then $f^{-1}={(a,1),(a,2)}$!

Theorem: let $f:A \to B$ be a function. Then $f^{-1}:B\to A$ exists provided $f$ is a bijection.

• need to be one-to-one, so that when reversed each input has only one image
• need to be on-to, so that when reversed each input has an image

Theorem: let $f:A\to B$ be a bijection. Then $f^{-1}$ is unique.

Proof: By contradiction, suppose there are two inverse functions $f^{-1}_1$ and $f_2^{-1}$

• then this means there is an element $f^{-1}_1(b) \neq f^{-1}_2(b)$
• but this means $f(f^{-1}_1(b)) \neq f(f^{-1}_2(b))$
• by definition, both $f_1^{-1},f_2^{-1}$ are inverse of $f$, so this cannot be right as we get $b \neq b$
• therefore, this is a contradiction and there can only be one unique inverse of $f$.

Pigeon Hole Principle

Given a function $f:A\to B$, recall that if $\vert A\vert > \vert B\vert$, then it must be some of the elements in $A$ going into the same image

PHP: if $p$ pigeons fly in $h$ holes, and $p > h$, then at least one of the hole contains two or more pigeons.

For example:

• We know that there are 8M people in NYC. We know that each person can have a maximum number of 300,000 hair strands. Then by PHP this means there are people having the same number of fair strands.

• Let there be three pairs of socks, B, G, R. How many socks do I need to blindly pick so that I get at least one pair?

  

• in a group of $n$ people, there will be always two people who have the same number of friends. Assume each person has at least one friend in this group. (Hint: the key is to realize the holes need to be “the number of friends”, and the maximum number of friends you can have is $n-1$)

• let $A = {1,2,3,4,5,6,7,8}$. If I pick 5 random numbers, will there be at least a pair of number that sums to $9$?

  the pigeons can be any five numbers $n_1,n_2,n_3,n_4,n_5$, the holes can be the pairs/the ways that sums to $9$.

Generalized PHP: Given $p$ pigoens and $h$ holes. If $p > h$ then at least a hole contains:

\[\lceil \frac{p}{h} \rceil \text{\ pigeons}\]

(the ceiling of $p/h$).

This also covers the PHP, because let $p=n$ and $h=n-1$. THen by GPHP we have $\lceil n/(n-1) \rceil = 2$ meaning at least one hole contains 2 pigeons.

Infinity and Countability

The aim is to discuss the size of a set who is infinite, but we saw in previous sections that if $f:A\to B$ is a bijection, then $\vert A\vert = \vert B\vert$

Countability: we say that set $S$ is countable $\iff$ there exists a bijection between $S$ and $\N$ (or some subset of $\N$).

• i.e. a set is countable, if you can enumerate all the elements without missing any

For example:

• let $S={10,20,30,40,50}$. This is countable, since we can take the image being ${1,2,3,4,5}$

• let $S={2,4,6,8,…}$. This is countable, as you as enumerate them as is.

• let $S={\frac{a}{b}\vert a,b\in \Z \land b \neq 0}$. How do you enumerate the values of fractions? George Cantor showed this $\Q$ is countable using diagonalization.

  First, we show $\Q+$ is countable

  	1	2	3	…
  1	1/1	1/2	1/3	…
  2	2/1	2/2	2/3	…
  3	3/1	3/2	3/3	…
  …	…	…	…	…

  • so I cannot enumerate by row, as I will never come back from a row. same reason for column
  • but I can go by a diagonal

  

  therefore:

  \[\{ 1/1, \quad 2/1, \quad 1/2, \quad 3/1,\quad 2/2, \quad1/3, ... \}\]

  so essentially countability can be seen as to find a strategy to enumerate it = can find a bijection from $\N$ by just corresponding each element here to a number in $\N$ (you do not need to know what that function is, but it can be enumerated).

  Finally to get $\Q$, we just need to insert each number’s negative in between.

Theorem: the set of real numbers $\R$ is not countable.

Corollary: the set of real numbers in $[0,1]$ is also not countable.

Proof: by contradiction using diagonalization.

• assume I can list all the real numbers in $[0,1]$, so that ${r_1, r_2, r_3, …}$, e.g.
  • $r_1 = 0.4513201…$
  • $r_2=0.3351238…$
  • $r_3 = 0.1234223…$
  • …
• we can show that this is missing at least one real number, by
  • let $\text{decimal}i(r{new})$ be the $i$-th decimal number of $r_{new}$. E.g. $\text{decimal}3(r{1})=1$ above.
  • I can invent a $r_{new}$ to be $\text{decimal}i(r{new}) \neq \text{decimal}i(r{i})$ for every $i$! e.g. $r_{new}=0.544…$
• and the key is this $r_{new}\in R$! (therefore this won’t work with proving $\Q$ being uncountable, though we already know it is not)

Advanced Proofs

Here we cover more techniques to prove things. We will cover

• proof by mathematical induction (PMI)
• proof by smallest counter example (PSCI)
• proof by strong mathematical induction (PSMI)

Proof by Induction

Consider proving propositions that look like

\[\forall n\quad p(n),\quad n \in \Z^+\]

The idea is to consider:

1. base case show $p(a)$ is true

2. if we can show $p(k) \implies p(k+1)$.

3. then $\forall k \ge a \implies p(k)$. It is like a “chain reaction”.

   

4. hence we have shown that $\forall n \in \Z^+ \quad n\ge a \implies p(n)$

Proof Template for Induction

1. write the proposition clearly

   \[\forall n \quad p(n)\]
2. \[p(a),\quad \text{a is the smallest case of n}\]

4. [inductive step] prove that “all the next steps/domino” are true given $p(k)$

   \[p(k) \implies p(k+1)\]

   here is when you can technically use all the different proof techniques (e.g. by contrapositive). But often we just do direct proofs.

5. therefore, $p(k)$ is true $\forall k \ge a$

For Example: prove that $\forall n \in \Z^+$

\[p(n): 1+2+3+ \dots + n = \frac{n(n+1)}{2}\]

Proof by induction: the proposition is already written in the “standard” format

1. base case is $p(1)$. This is true because

   \[p(1): 1 = \frac{1\cdot 2}{2}\]

   is true

2. inductive hypothesis that for $k \ge 1$, we assume $p(k)$ is true

   \[p(k):1+2+3+\cdots + k = \frac{k(k+1)}{2}\]

3. inductive step so $p(k+1):1+2+3+\cdots + k + k+1= \frac{k+2(k+2)}{2}$ and it requires you to prove that $p(k+1)$ is true by

   \[p(k) \implies p(k+1)\]

   we can consider a direct proof

   1. let $p(k)$. This means this is true

      \[1+2+3+\cdots + k = \frac{k(k+1)}{2}\]

   2. then this means

      \[1+2+3+\cdots + k + k+1 = \frac{k(k+1)}{2} + k+1\]

      this step can be interpreted in two ways (both valid)

      • smudging the entire $p(k)$ to look like $p(k+1)$
      • just want to see what does RHS look like by $1+2+3+\cdots + k + k+1 = p(k)+k+1$

   3. rewriting the RHS we get

      \[1+2+3+\cdots + k + k+1 = \frac{(k+2)(k+1)}{2}\]

      which is exactly $p(k+1)$

   4. hence, we have shown that $p(k+1)$ is true assuming $p(k)$, i.e. $p(k)\implies p(k+1)$

For example: prove that $\forall n \in \Z, n \ge 1$

we want to show that

\[1+3+5+\dots+(2n-1) = n^2\]

Visually, this looks like

Proof by induction:

1. base case is $p(1)$. This is easily true since $1=1^2$

2. inductive hypothesis: assume $p(k)$ is true

   \[1+3+5+\dots+(2k-1) = k^2\]

3. inductive step: want to show that $p(k+1)$ is true given $p(k)$, so that considering direct proof

   1. let $p(k)$ be true, hence

      \[1+3+5+\dots+(2k-1) = k^2\]

   2. then moving to $p(k+1)$ we get

      \[1+3+5+\dots+(2k-1)+(2k+1) = k^2 + 2k+1\]

   3. the RHS can be reformatted to be

      \[1+3+5+\dots+(2k-1)+(2k+1) = (k+1)^2\]

   4. this is basically $p(k+1)$

Well-ordering principle: every set of non-negative integers has a starting element (i.e. a beginning)

• The induction process is possible thanks to the principle of well-ordering principle.
• this does not necessarily have to be the smallest element. e.g. prove in the domain of only negative numbers you can start with the largest element, and prove $p(k)\implies p(k-1)$

For example:

• is well-ordering: $\N={1,2,3,…}$, $S={4,5,6,…}$
• not well-ordering: $\R$, $\Q$, or even $\R^+$.

Proof by Smallest Counter Example

To compare this with what you

PMI: essentially proves the purple ones

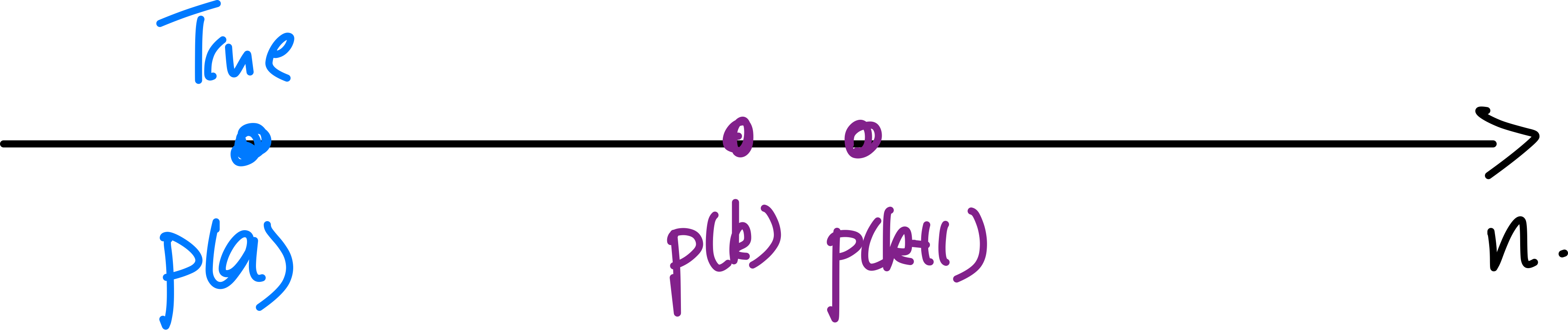
PSCI: aims to prove the red one being false, hence there cannot be a CE:

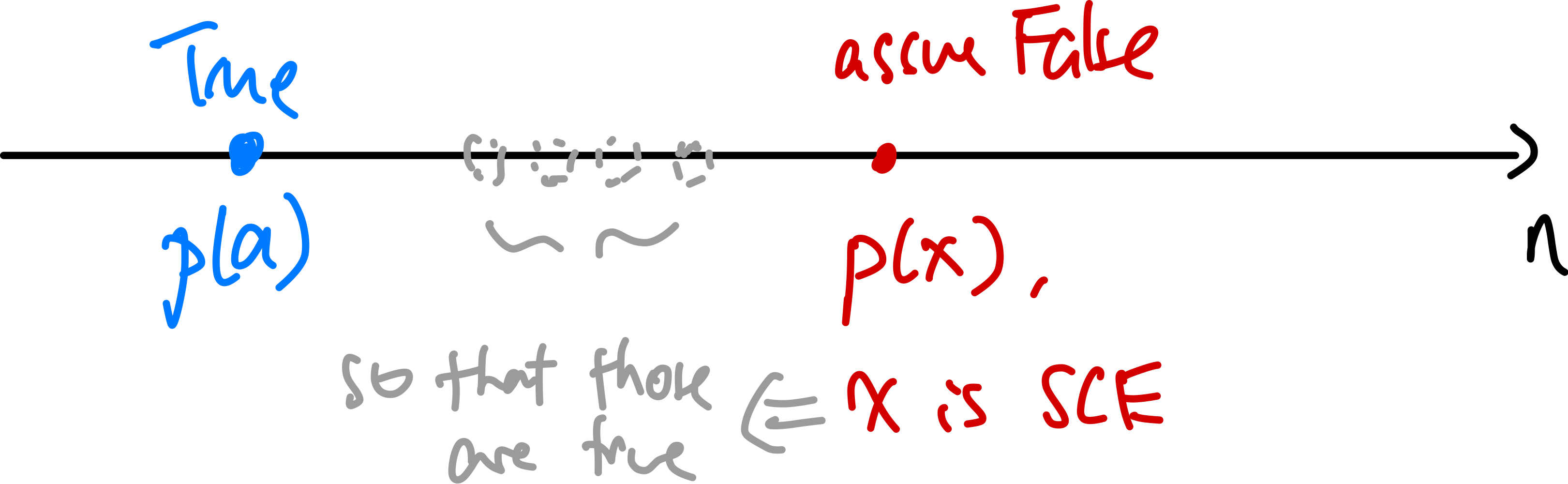
Proof Template for PSCI

1. write in $\forall n \quad p(n)$

2. prove base case

3. assume that there exist exceptions/counter examples. Let $x$ be the smallest so $p(x)$ is False. Notice that this also means $p(x-1)$ is true

4. prove that this is a contradiction, hence $p(x)$ cannot exist. i.e. this cannot hold.

   \[p(x)\text{ is False } \land\,\, p(x-1)\text{ is True }\]

5. if there is no SCE, then there is no CE at all given the well-ordering principle. Hence the proposition is true.

Proof by SCE: show that

\[p(n): 1+2+3+ \dots + n = \frac{n(n+1)}{2}\]

1. base case $p(1)$ is true since $1=1\times 2/2$

2. by contradiction, assume that $\exists x > 1$ such that $p(x)$ is False, for $x$ is the smallest counter example

3. then we can show that this is a contradiction that this cannot happen. So that given

   \[p(x):1+2+3+ \dots + x \neq \frac{x(x+1)}{2}\]

   but that

   \[p(x-1):1+2+3+ \dots + x-1 = \frac{x(x-1)}{2}\]

   cannot hold.

4. therefore, there is no SCE, meaning essentially

   \[\neg (\exist x > 1 \quad p(x) \text{ is False})\]

   so that for $n \in \Z^+$

   \[\forall n \quad p(n)\]

Proof by SCE: prove by SCE that

\[\forall n \in \Z, \quad n>0 \to 4|(5^n-1)\]

1. base case $n=1$ works easily

2. by contradiction, assume $x$ the S.C.E such that $p(x)$ is false. i.e. $4$ does not divide $5^x-1$

   \[4 \nmid (5^x-1)\]

3. now we want to show that this is a contradiction: $p(x)$ is false and $p(x-1)$ is true cannot hold

   1. since $p(x-1)$ is true, this means $4\vert (5^{x-1}-1)$

   2. this means $5^{x-1}-1=4\times q$, where $q \in \Z$. We want to move towards contradiction that $4 \nmid (5^x-1)$

   3. multiply by 5, we get

      \[5^x-4-1 = 4\times (5 \times 1)\]

      hence

      \[5^x-1 = 4 \times( 5 \times q + 1)\]

      meaning that $4 \vert (5^x-1)$

4. therefore, there is no such $x$ such that $p(x)$ is false. Hence the proposition is true.

Proposition: Every Integer is either odd or even.

Note that now we are considering $\forall n \in\Z$, meaning there is technically not a “well-ordering set”. But there can be a trick:

1. first prove by SCE that this holds when $\forall n \in \Z^+$

2. extend your above proof to the negative domain, since

   \[n \in \Z,n < 0 \implies n = -m, m\in \Z^+\]

   basically flipping the sign

Proof by Strong Induction

The difference with proof by induction is:

• could have many base cases
• making stronger assumptions that all cases from the base cases until $p(k)$ are true. Prove $p(k+1)$

Graphically, it looks like:

Method	Visual
normal Induction
strong induction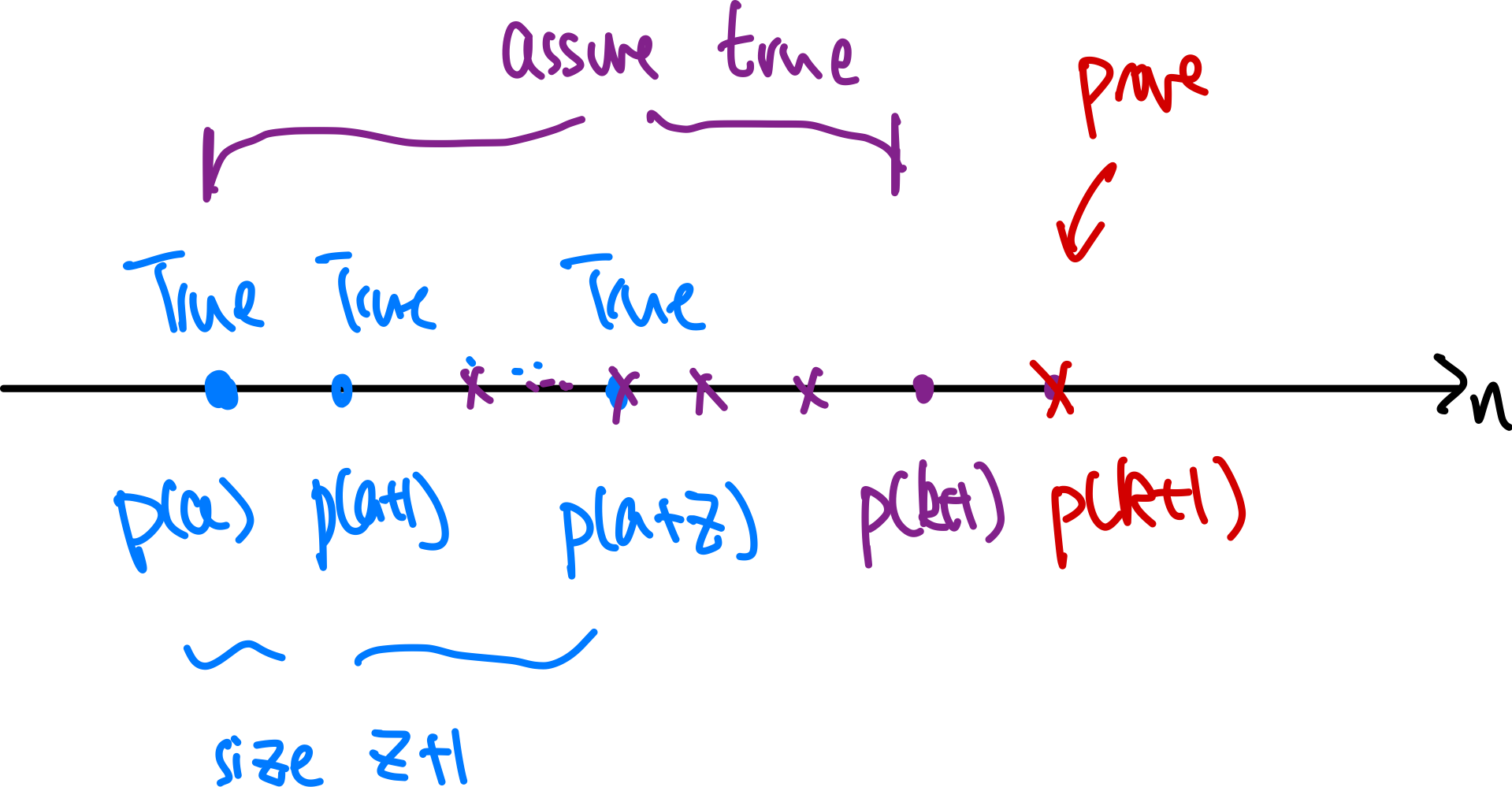

and finally this also means base case for strong induction has to look like:

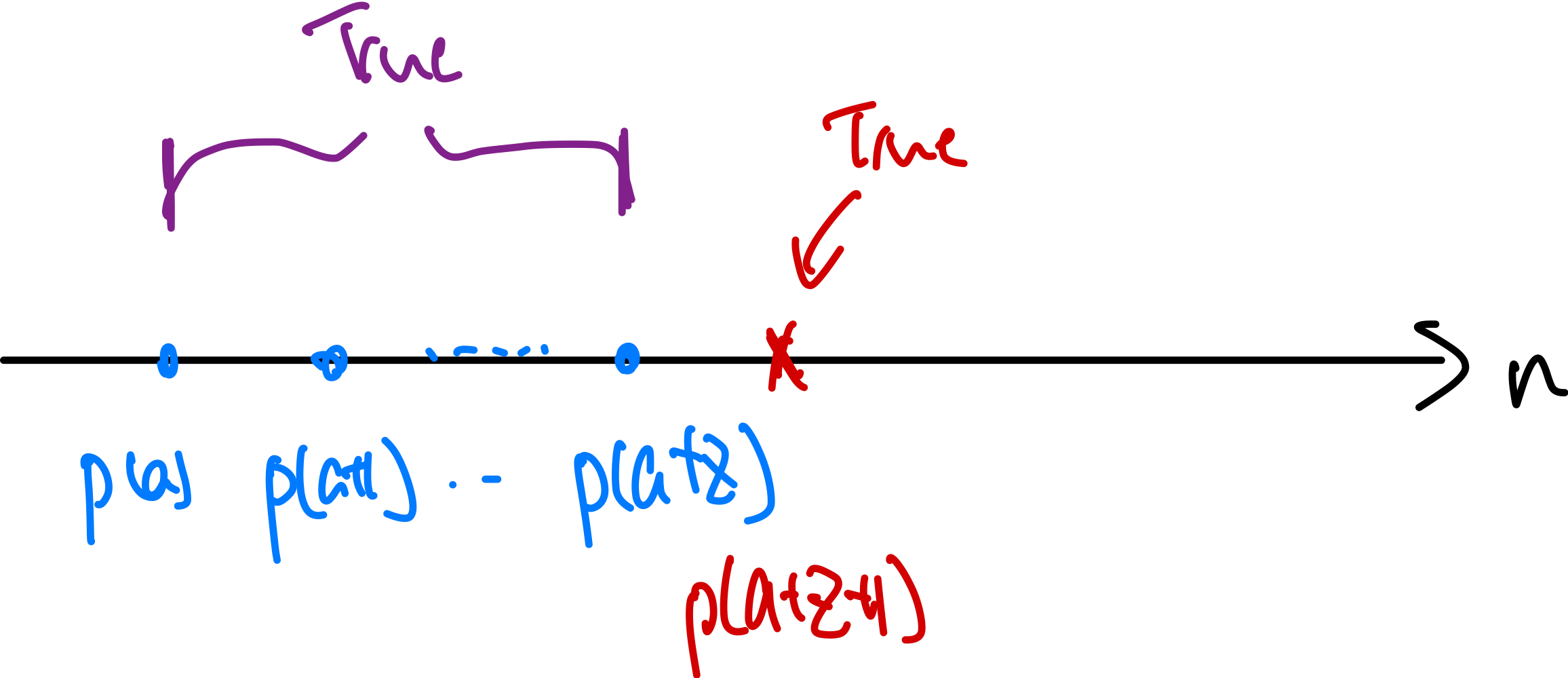
Therefore, this is useful when the result for $n = k+1$ depends on the result for some smaller value of $n$ (e.g. $n=k-4$), but it’s not the immediately previous value $k$.

Proof Template for PSI: consider proving some $\forall n \quad p(n)$

1. base case: prove the base cases (you will need to experiment to find out how many you need)

   \[p(a),p(a+1),p(a+2),...,p(a+z)\]

2. inductive hypothesis: assume $p(k)$ hold for all numbers less than or equal to an arbitrary $k$, i.e. all the below are true

   \[p(a) \land p(a+1)\land \dots p(k)\]

   (i.e. the purple window above)

3. inductive step: now it becomes

   \[p(a) \land p(a+1)\land \dots p(k) \implies p(k+1)\]

   essentially to prove $p(k+1)$ you have a range of choices/assumptions to choose from. (see example below)

   • The difference is actually only superficial compared to normal induction proofs, and the two proof techniques are equivalent.
   • you can see this more in the example below

   and you want to make sure $p(a+z+1)$ can be proven using this inductive step (where $p(a+z)$ you already show to be true in step 1)

   • this usually depends on, say $p(k+1)$ required $p(k-3)$ to be true.
   • so this means you need $p(k), p(k-1),p(k-2),p(k-3)$ to be true = need 4 base cases in step 1 for arbitrary $k$ to hold

4. conclusion: repeatedly apply the above proof to increase the purple window until all $\forall n$ are covered. (same as normal induction)

Example: Stamping Problem. Prove that any amount of postage $\ge 2$ cent can be made with 2 cents or 3 cents stamp.

Let’s first attempt using simple induction.

1. base case: I can make $p(2)$ with one stamp of 2 cent
2. inductive hypothesis: it is possible to make a postage worthy of $k$ cent using 2 or 3 cents stamp
3. inductive step: prove $p(k+1)$, show that you can make $k+1$ cent
   • case 1: $p(k)$ has only 2 cents stamp. Take a 2 away and replace by 3 cents.
   • case 2: $p(k)$ has only 3 cents stamp. Take a 3 away and replace by two 2 cents.
   • case 3: $p(k)$ has both 2 cents and 3 stamps. Take a 2 away and replace by 3, or take a 3 and replace by two 2 cents.
4. done.

Let’s see how strong induction would prove this:

1. base case: we will see how many cases we need. First prove (skipped) that $p(2),p(3),p(4),p(5)$ are true

2. inductive hypothesis: by assumption then let the following until $k$ be true

   \[p(1) \land ... p(6) \land p(7)\dots p(k)\]

3. inductive step: to prove $p(k+1)$ all I need is to show

   \[p(1) \land ... p(6) \land p(7)\dots p(k) \implies p(k+1)\]

   realize that

   \[p(k+1) = p(k-2+3)=p(k-2)+3\]

   i.e. adding a 3 cent in the solution for $p(k-2)$. Since $p(k-2)$ is true by inductive hypothesis, we are done.

   • This also means we need at least 3 base cases, that $p(2),p(3),p(4)$ is already proven (it is)
   • since we need the left boundary of our purple window at $2 \le k-2$, so $k\ge 4$. Therefore we needed base case up to $p(k=4)$

4. therefore $p(k+1)$ is true.

Notice that we needed to directly prove (a minimum of) three base cases, since we needed to reach back three integers in our inductive step. It’s not always obvious how many base cases are needed until you work out the details of your inductive step.

Number Theory

Here we will discuss topics including

• divisibility
• GCD/GCF (greatest common divisor/factor)
• fundemental theorem of arithmetic
• factoring
• modular arithmetic (clock arithmetic)
• introduction to cryptography

Divisibility

In the 1880, Peano’s axioms of natural numbers (converted into natural language):

1. there is a starting point of numbers $x \in \N$, and it starts at 1

2. let $s$ be a successor function. Every natural number has a successor:

   \[\forall n \in \N, \quad s(n) \in \N\]

3. and 1 is not a successor of any natural number, so that $1 \neq s(n)$

4. let $s(n)$ is a one-to-one function., so that each number has a different successor.

5. there is no other set of natural numbers.

These requirements enabled a “massive production of numbers”, and they have some interesting consequences

Divisibility Theorem: let $a,b \in \Z$, and $b > 0$, then there exist a unique pair $(q,r)$ such that

\[a = bq +r,\quad 0 \le r < b\]

note that $r,b$ is positive.

for example:

• $25 = 10\times 2 +5$, where $25=a$, $b=10$, etc.
• $-25 = 10 \times -3 +5$. Note that both $b$ and $r$ are positive.

for example: prove that every integer is either odd or even

1. by the divisibility theorem, there is a unique pair $(q,r)$, such that

   \[n = 2q + r,\quad 0 \le r <2\]

2. i.e. if I divide by 2, the remainder can only be zero or one! then,

   • if $r=0$, this means $n=2q$ hence $n$ is even
   • if $r=1$, this means $n=2q+1$ hence $n$ is odd.

Div and Mod Operators: let $a,b \in \Z, b > 0$. We know that $a = bq +r,\quad 0 \le r < b$ .Then

\[\exists (q,r) \in \Z \times (\Z^+ \cup \{0\})\]

and then we define the operators

• $a \mathrm{\ div\ }b = q$
• $a \mathrm{\ mod\ }b = r$

Least Common Multiple and Greatest Common Divisor

Proposition: let $a,b \in \Z$,. Let let $d\in \Z^+$ means

\[d|a \land d |b \implies d|(a+b) \land d|(a-b)\]

i.e. $d$ also divides any linear combination of $a,b$. This is very useful as it means, for example:

\[gcd(a,b)≡gcd(−a,b)≡gcd(a,−b)≡gcd(−a,−b)≡gcd(∣a∣,∣b∣)\]

The above comes useful in later proofs. This proposition is itself relatively easy to prove, since:

• to prove $d\vert (a+b)$ you can rewrite $a+b=dq_1 + dq_2=d(q_1+q_2)$ since $d\vert a \land d\vert b$
• to prove $d\vert (a-b)$ you can rewrite $a-b=dq_1 - dq_2=d(q_1-q_2)$ since $d\vert a \land d\vert b$

Greatest Common Factor/Divisor: let $a,b \in \Z$. We call $d$ the greatest common factor IFF

1. $d \vert a \land d\vert b$ (i.e. is a divisor)
2. $\forall e \in \Z, \quad e\vert a \land e \vert b \implies e \le d$ (i.e. is the biggest)

For example: there are 28 roses, 14 daisies. What is the greatest number of identical bouquet of flowers can you make with no flowers left?

• let there be $k$ bouquet of flowers. Realize this $k$ must be a divisor such that $k\vert 28$ and $k\vert 14$
• to have the most $k$, you basically need to find the greatest common divisor. In this case you can find by inspection, giving $14$.

Properties of GCD

• $\mathrm{GCD}(a,0)=a$, since divisor for $0$ includes all numbers
• $\mathrm{GCD}(0,0)$ is undefined
• $\mathrm{GCD}(a,b)=\mathrm{GCD}(b,a)$
• $\mathrm{GCD}(a,b)=\mathrm{GCD}(\vert a\vert ,\vert b\vert )$
• $\mathrm{GCD}(a,b,c)=\mathrm{GCD}(a,\mathrm{GCD}(b,c))$.

But how do we find GCD?

Naive GCD: without loss of generalization, let $a \ge b$. Then

1. for each $d=1$ to $b$ (in case of co-prime, $\mathrm{GCD}(a,b)=1$ )
   1. if $d\vert a\land d\vert b$ then $g=d$
2. return $g$

Before we discuss a more efficient algorithm: observe: let $a,b\in \Z^+$. Realize that $\mathrm{GCD}(a,b)=\mathrm{GCD}(b,a \mod b)$.

• $\mathrm{GCD}(75, 63)=\mathrm{GCD}(63, 12)$
  • note that if you started with $\mathrm{GCD}(63, 75)\to\mathrm{GCD}(75, 63)$ since $63 \mod 75=63$ gets automatically swapped.
• but you can continue: $\mathrm{GCD}(63, 12)=\mathrm{GCD}(12, 3)=\mathrm{GCD}(3, 0)$
• then you are done. GCD is 3!

Graphically:

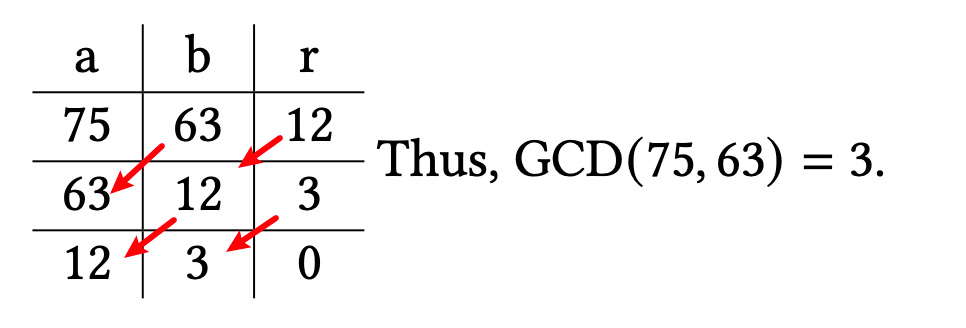
Essentially at each iteration you managed to cut the “search space”!

Euclid GCD Algorithm: let $a,b\in \Z^+$. Realize that $\mathrm{GCD}(a,b)=\mathrm{GCD}(b,a \mod b)$ as shown above (proof later). Then the algorithm becomes

def recursive_gcd(a,b):
    r = a mod b
    if r = 0:
        return b
    else:
        recursive_gcd(b, r)

but you can of course write this into an iterative version

def iterative_gcd(a,b):
    r = a mod b
    while r != 0:
        a = b
        b = r
        r = a mod b
    return b

Proof of Euclid’s divisibility. The key is to utilize divisiblity that, consider $\mathrm{GCD}(a,b)$ then

• $a=bq +r$, with $0 \le r <b$ by divisibility
• hence $r=a-bq$ i.e. by definition, $r$ is basically $a \mod b$

Therefore, the proof looks like

1. let $d$ be a divisor of $a$ and $b$. Then $r=a-bq$ means that
   1. $d\vert a \implies a=d\cdot q_1$, and $d\vert b \implies b = d\cdot q_2$
   2. hence $r=dq_1 - qdq_2 = d(q_1 - qq_2)\implies d\vert r$
   3. so any divisor of $a,b$ is also a divisor of $r$
2. let $c$ be a divisor of $b$ and $r$. Then $a=bq + r$ means that
   1. similarly you can show that $c\vert a$
   2. so any divisor of $b,r$ is also a divisor of $a$
3. form the above two conclusions, $a,b$ and $b,r$ have the same common divisors. (e.g. let $k$ be a common divsor for $a,b$ but not for $b,r$. Then this means $k \nmid r$, which cannot be due to our proof above!)
4. Hence $\mathrm{GCD}(a,b)$ ad $\mathrm{GCD}(b,r)$ must be the same/share the same GCD!

Prime Numbers and Factorization

The idea is that

\[\N = \{1,2,3,\dots\} = \{1\}\cup \text{primes}\cup \text{composites}\]

and that interestingly:

• primes are more “dense” when small
• there is an infinity amount of prime numbers

Fundemental theorem of arithmetic: let $n \in \Z \land n \ge2$. There is a unique factorization of $n$ into a product of primes. i.e. $n$ is either a prime of a product of primes (composites).

To prove the above, you will need to show that

1. there exists a prime factoriazation for any $n \ge 2$
2. this factorization is unique (this can get quite complicated to prove, see Gauss’s proof)

Proof: there exists a prime factorization. Proof by strong induction

1. base case: let us use $p(2)=2,p(3)=3,p(4)=2\times 2$ have a prime factorization.
2. inductive step: every number between $2$ and $k\ge 5$ can be factored into primes
3. prove $k+1$: realize either that $k+1$ is a prime or a composite.
   • if $k+1$ is a prime, then $p(k+1)=k+1$, done.
   • if $k+1$ is a composite
     • then $k+1 = a\times b$ for some factors $a,b<k+1$. (technically this can be even strong that $a,b< (k+1)//2$, but it is not necessary)
     • but realize that we have assumed $p(a)$ and $p(b)$ are both having a prime factorization
     • hence $k+1$ also has a prime factorization
4. therefore, $k+1$ also has a prime factorization.

Theorem: there is an infinite number of prime numbers.

Kumer’s proof: proof by contradiction. Suppose there is a finite number of primes:

\[p_1 < p_2 < \dots < p_r\]

where $p_r < \infty$ is finite. Then

1. $x=p_1\times p_2 \times \dots \times p_r$ is a composite included all possible primes
2. consider $x+1=p_1\times p_2 \times \dots \times p_r+1$
   • if $x+1$ is prime
     • we already get a contradiction $x+1 > p_r$
   • if $x+1$ is a composite
     • then since $x$ is a composite including all primes, $x$ and $x+1$ must share at least a prime, let’s call this $p_i$
     • then $p_i\vert x$ and $p_i \vert (x+1)$, so that $x=p_iq_1$ and $x+1 = p_i q_2$
     • $x+1-x=p_i q_2 -p_iq_1$ hence $1 = p_i(q_2-q_1)$
     • but $p_i\vert 1$ cannot be true as the smallest prime number is $2$!
     • this is a contradiction
3. Hence, by contradiction there is an infinite number of primes.

Sieve of Fratosthenes: what is a good way to find all primes until $n$? E.g. let us find all primes less than $n=20$

1. write down every integer $2,3,\dots,20$
2. for $i$ each of the above integer that is not crossed out
   1. cross out all multiples of $i$
   2. stop at $\lfloor \sqrt{n} \rfloor$, because the biggest possible factor is $\lfloor \sqrt{n} \rfloor$
3. whatever not crossed out are the primes

Graphically, if you pick $n=41$:

Finally, prime factorization can be used as a good way to find GCD by hand:

so basically all you need to do is to pick the minimum power. This would be useful when you need to find GCD by hand/both $a,b$ are relatively small. Otherwise using the Euclid algorithm should be much faster.

Note: what is the relationship between $a \mod b$ and $a-b$?

• since $a=qb + r$, this means $a \mod b = a - b -b -b \dots -b$ with $q$ number of $b$s
• this also means if $a/2 < b$, then $q=1$, hence $a \mod b = a - b$

Modular Arithmetic

In many applications such as clock, month, cryptography in $\Z_n = {0,1,2,\dots, n-1}$, we need a “new” type of arithmetic to say something like $n+3 \to 2$ (e.g. 14pm is the same as 2pm)

• this should remind you of the congruence modulo $n$

• for example, clock would have $\Z_{12}={0,1,2,\dots, 11}$ and has 12 equivalence classes

  • e.g. $\dots, -24,-12,0,12,24,\dots$ (given any number outside of the range, either plus 12 or minus12 until you get back into $\Z_{12}$)
  • e.g. $\dots, -23,-11,1,13,25,\dots$

Then defining the “arithmetics”:

• addition in $\Z_{n}$: let $a,b\in \Z_{n}$, then

  \[a \oplus b \equiv (a+b) \bmod {n}\]

  e.g. let $n=10$, then $12\oplus 12 = 24 \bmod 10 = 4$.

• multiplication: same thing, let $a,b\in \Z_{n}$,

  \[a \otimes b \equiv (a\times b ) \bmod n\]

• subtraction: now the problem is with $a,b\in \Z_{n}$, you can get negative numbers in the sense that:

  • if $a - b > 0$, then $a \ominus b = (a-b)\bmod n$
  • if $a - b < 0$, then $a \ominus b = (a-b)+n$ (i.e. add as many $n$ until you get back into $\Z_{n}$, in this case since $a,b\in \Z_n$, add once is enough)
    • e.g. let $n=10$, then $1-4 = -3 + 10 = 7$

• division: same setup, but recall that

  • in normal arithmetic we have $a / b = a \times b^{-1}$, where the reciprocal $b^{-1} = 1/ b$.

  • here, we want to consider

    \[a \oslash b = a \otimes b^{-1}\]

    and that by definition, the reciprocal has to satisfy $b^{-1}\otimes b = 1$. Any element in $\Z_n$ that has a reciprocal is called invertible in $\Z_n$). Therefore, this division only exists when $b$ is invertible.

    • for example, for $\Z_{10}$, only the following ${1,3,7,9}$ has inverse.
    • you will see how this is related to coprimes.

  How do we find the inverse in this new arithmetic?

  • e.g. let $n=10$. Then $2 \oslash 7 = 2 \otimes 7^{-1} = 2 \otimes 3 = 6$, because $7^{-1}\times 3 = 21 \bmod 10 = 1$ is invertible!

Is there a systematic/mathematical way to find the inverse?

Coprime: let $a,b\in Z^+$. We call $a,b$ being coprimes IFF $\gcd(a,b)=1$. We denote this with $a \perp b$.

• this is a generic definition for all $\Z^+$
• in the case of modular arithmetic, the only invertible elements in $\Z_n$ are the coprimes with $n$

Then, to find the inverse you can use:

Extended GCD Algorithm: let $a,b,d \in \Z^+$. It turns out that if

\[d|a \land d |b \land d= ax+by,\quad \text{for some $x,y\in \Z$}\]

then

\[\gcd(a,b) = d\]

in other words, you can always write $\gcd(a,b)$ as $\gcd(a,b)=ax+by$!

How can this be true? Proof:

• for any common divisor $d\vert a \land d \vert b$, so $d \le gcd(a,b)$ obviously
• but I also said $d = ax+by$. So any common divisor of $a,b$ must divide $d$. This means $gcd(a,b)$ divides $d$, hence $d \ge gcd(a,b)$
  • i.e. $d$ = any common divisor times something positive.
• since $gcd(a,b) \le d$ and $\gcd(a,b) \ge d$, hence $gcd(a,b)=d$

For example: considering finding $\gcd(41,43)$, and show $\gcd(41,43)=41x+43y$

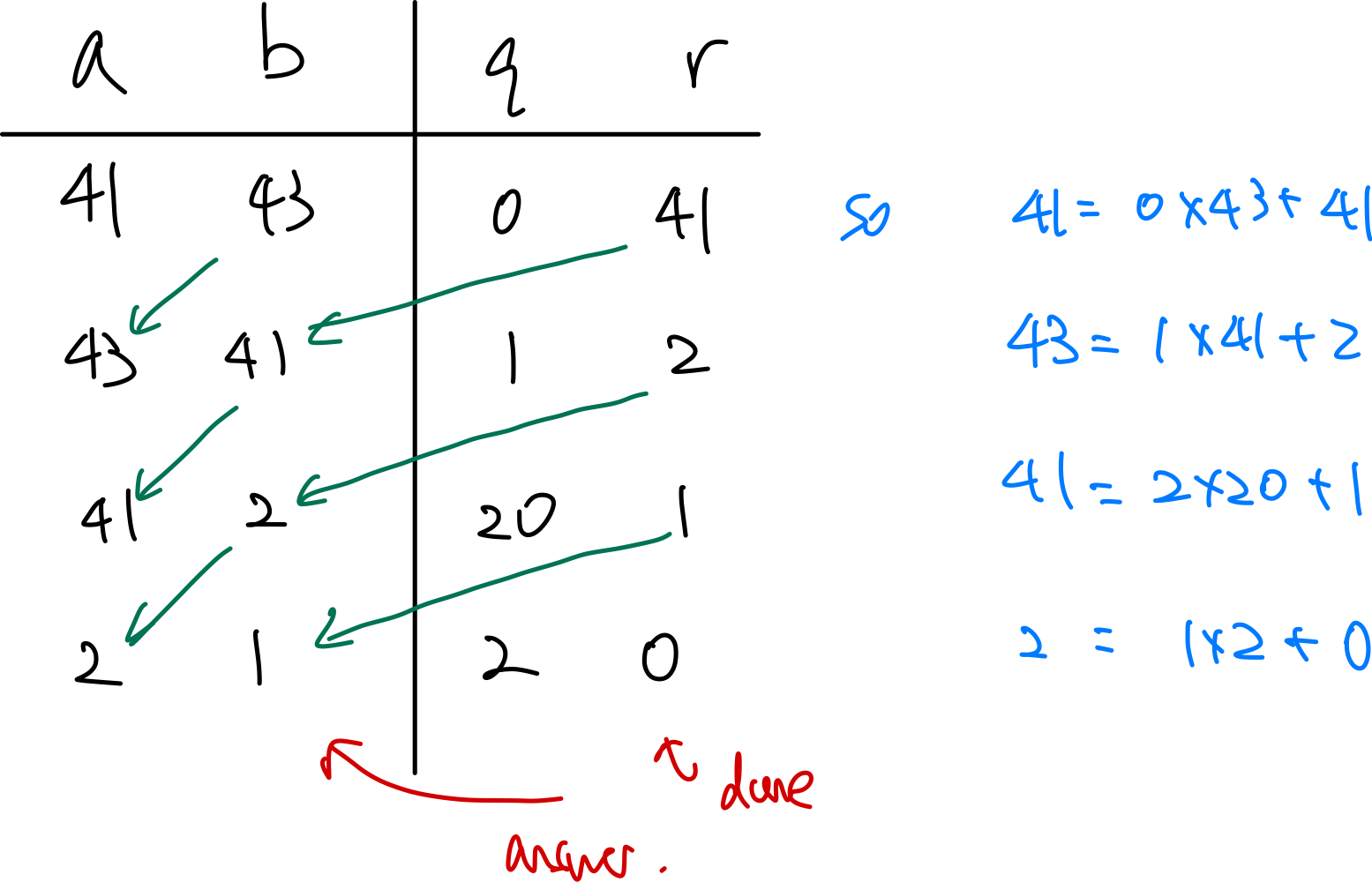
we want to show $\gcd(a,b)=ax+by$.

• since $\gcd(41,43)=1$ in the last step

• If I take the second and third step, we have $43= 41\times 1 + 2 \implies 2 = 43 - 41 \times 1$, and $41=2\times 20 + 1 \implies 1 = 41 - 2 \times 20$.

• hence I just substitute them in $1 = 41 - (43 - 41)\times 20 = 21 \times 41 - 43 \times 20$, hence

  \[\gcd(43,41) = 1 = 43 \times (-20) + 41 \times (20) = ax + by\]

Modulus Division: this is a consequence of extended GCD + all invertible elements in $\Z_n$ are coprimes. Therefore, take any invertible element in $\Z_n$ we have:

\[\gcd(a,n)=1 = ax + ny\]

therefore, notice that in modular arithmetic $ny$ goes away, hence:

\[a\otimes x = 1\implies x = a^{-1}\]

finally, you want to be careful that $x \in \Z_n$ by mapping it back.

For example,

• what is $41^{-1}$ for $\Z_{43}$? We know that

  \[\gcd(43,41) = 1 = 43 \times (-20) + 41 \times (20)\]

  therefore, $41^{-1}=20$.

• what is $3^{-1}$ for $\Z_{40}$? Given that

  \[\gcd(3, 40) = 1 = 3 \times (-13) + 40 \times (1)\]

  therefore, $3^{-1}=13 + 40=27$

Public Key Cryptography

Here we discuss the basics of RSA

1. Bob will pick two large prime numbers $p,q$, such that $n=p \times q$

2. Bob chooses an $e$ that is coprime with $(p-1)$ and $(q-1)$ so that

   \[\gcd(e, (p-1)(q-1)) =1\]

   and also knows $d=e^{-1}$ is invertible (and easy to find knowing $p,q$). This is the secret key.

3. the public key is invertible, $n,e$ is sent to Alice (and everybody can see the two). This is public key.

4. Alice then prepares the encrypted message and encrypt it with $e$ to get $E(m)=m^e \bmod n$

5. Bob then inverts this by, recall that $e\otimes d=1$, hence

   \[E^{-1}(E(m)) = (m^e)^d \bmod n = m\]

   decodes it back.

So the key idea is you need $d$ to decode, but finding $d=e^{-1}$ will take years to compute if you don’t know it (or $p,q$) in advance.

Counting

Here we will talk about

1. counting lists: arrangements, permutations, anagrams
2. counting sets: combination, pascal triangle, binomial coefficients

Counting Lists

Multiplication Theorem: the number of lists of length $k$ where elements can be chosen from a set of $n$ possible elements is

\[\begin{cases} n^k, & \text{if repetitions are allowed}\\ (n)_k \equiv n!/(n-k)!, & \text{if repetitions not allowed} \end{cases}\]

where $(n)_k$ is called the fallen factorial because it does not go all the way down to $1$. This is basically permutations.

Essentially we are constructing lists = order matters = permutations.

For example:

• making phone numbers (list of length $10$) from all numbers $0\sim 9$ with repetition is $10^{10}$.
• making phone numbers (list of length $4$) from all numbers without repetition is $(10)_4 = 10! / 6!$
• if you have $5$ shirts, $3$ pants, and $4$ pairs of shoes, how many outfits can you make? $5\times 3\times 4$.

Anagrams: a permutation of the letters in a word, without repetition.

for example:

• how may anagrams can you create from “math”? $4!=24$ ways
• what about from “momo”? We need to be careful of duplicates created by repeating “m” ($2!$ ways) and “o” ($2$! ways). Therefore $4!/(2!\times 2!)$

We can write the above process in a general formula:

\[\frac{n!}{n_1!\times n_2!\times \dots \times n_k!} = \frac{n!}{\Pi_{i=1}^k n_i!}\]

where there are $k$ unique letters, and each of those letters repeated $n_k$ times.

Counting Sets

Now, we want combinations of $k$ elements taken from a set of $n$ possible element. Since we are counting sets = order does not matter

Combination: the set of $k$ elements sets of $n$ elements of an $n$-element set such that $0 < k \le n$ is called a combination

Binomial Coefficient: let $n,k>0$. A binomial coefficient denoted as

\[{n \choose k} = \frac{n!}{(n-k)!k!} = \frac{(n)_k}{k!}\]

is the number of combinations of choosing (sets of $k$ elements) from $n$ elements. $k!$ represents, given a permutation $[a,b,c]$, the number of ways you can double count if you are counting combinations.

Why is it called binomial coefficients? Consider $(x+y)^k$. Then essentially you get

\[(x+y)^k = \underbrace{xx...xxx}_{\text{length $k$}} + xx...xxy + xx..xyy + \dots + yy...yyy\]

therefore, to collect terms into $x^iy^{k-i}$, it becomes a combination problem $k\choose i$. Therefore you also get

Binomial Theorem: let $n\in \N$, then

\[(x+y)^n = \sum_{k=0}^n {n \choose k} x^{n-k}y^k\]

Pascal’s triangle: visually you can decompose a combination $n \choose k$ into two terms:

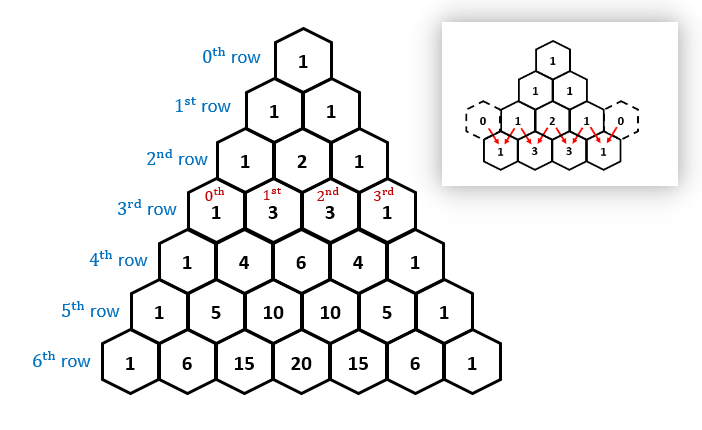
For example, we have on the 3rd row ${3 \choose 0}=1$ and ${3 \choose 1}=3$, etc, but realize that:

\[{3 \choose 1}= {2 \choose 0}+ {2 \choose 1}\]

Pascal’s Identity: for $n,k\in \Z$, and $0 < k < n$ is positive

\[{n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}\]

Intuitively, this works because:

• first ${n \choose k}$ represents finding sets of size $k$ out of $n$ distinct elements
• let there be a “special element $sp$” amongst the $n$ element. The ${n \choose k}$ means “sets of size $k$ that includes $sp$” + “sets of size $k$ that exludes $sp$”. Hence we get:
  • “sets of size $k$ that (already) includes $sp$” = choosing $k-1$ elements out of $n-1$
  • “sets of size $k$ that exludes $sp$” = choosing $k$ elements out of $n-1$

From the above you also see the symmetry of combinations

Rabbit property: the following are equivalent

\[{n \choose k} = {n \choose n-k}\]

this makes sense because, say you are choosing a team of $k$ members out of $n$ people. Then for each team of $k$ you choose, you also implicitly chose a team of $n-k$. Since there is a one-to-one mapping of the teams you choose/left out = equality.

Inclusion Exclusion Principle

This is essentially used to count size of union sets with arbitrarily large number of sets.

For example, let there be 4 sets,

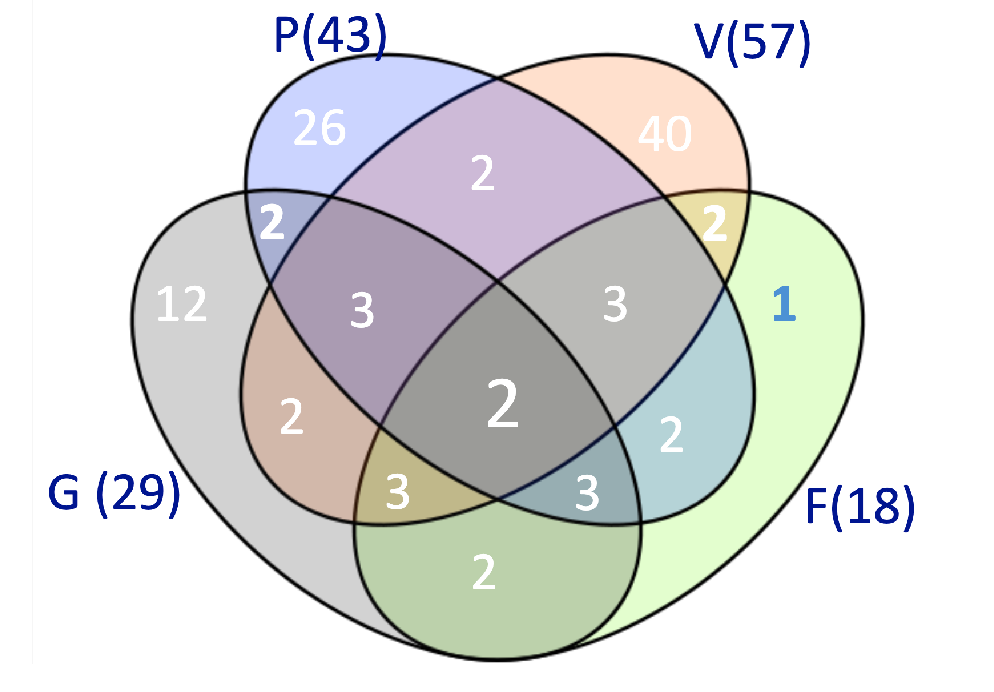
and you want to figure out the union size $\vert G \cup P \cup V \cup F\vert$?

The finding is that (without proof), let $A_1, …,A_n$ be finite sets, then

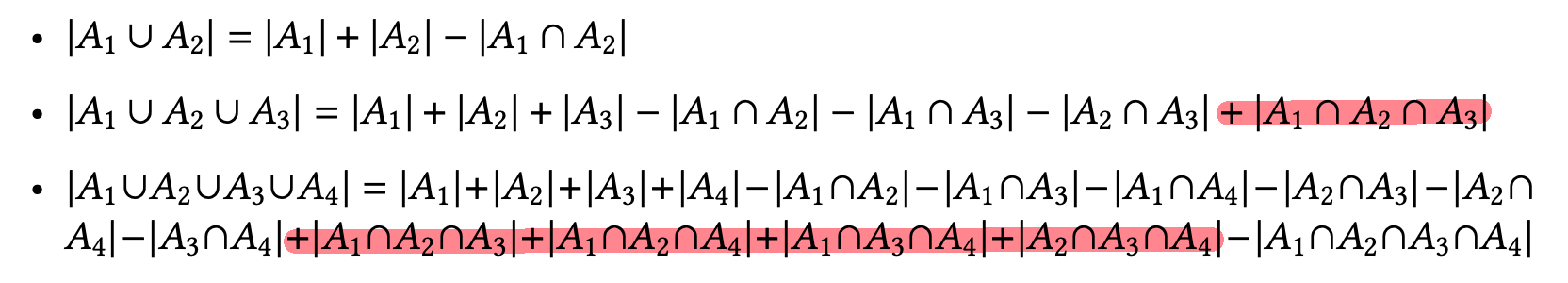
so the sign is alternating. This leads to a general formula

Principle of Inclusion/Exclusion (PIE): there is an alternating sign as the number of sets $\cap$ increases. Hence

\[\left| \bigcup_{i=1}^n A_i \right| = \underbrace{\sum_{i=1}^n |A_i|}_{\text{n choose 1 terms}} - \underbrace{\sum_{1\le i <j\le n} |A_i \cap A_j|}_{\text{n choose 2 terms}} + ...+\underbrace{(-1)^{n-1}|A_1 \cap ... A_n|}_{\text{n choose n terms}}\]

basically a formulaic way if there are large number of sets so that Venn diagram is not drawable.

For example: At the music academy, there are 43 students taking piano $A_P$, 57 students taking violin $A_V$, 29 students taking guitar $A_G$, and 18 taking flute $A_F$. There are 10 students in any two of these courses, 5 students in any three of them and 2 taking all courses. How many students are taking at least one course at the music academy?

This is equivalent of answering $\vert A_P\cup A_V\cup A_G \cup A_F\vert$, hence we get from PIE

• add $\vert A_P\vert + \vert A_V\vert + \vert A_G\vert + \vert A_F\vert$ already known

• minus $(\vert A_P\cap A_V\vert + \vert A_P \cap A_G\vert + …)$. Since “there are 10 students in any two of these courses” and there are 4 choose 2 ways to choose the two groups we get $10 \times {4 \choose 2}$
• add $(\vert A_P \cap A_V \cap A_G\vert + …)$ etc.

So we have

\[|A_P\cup A_V\cup A_G \cup A_F| = \underbrace{43+57+29+18}_{\text{1 term}} - \underbrace{10 \times {4 \choose 2}}_{\text{2 terms}} + \underbrace{5 \times {4 \choose 3}}_{\text{3 terms}} - \underbrace{2}_{\text{4 terms}} = 105\]

Graph Theory

We will focus on simple graphs, that are undirected, has no loops (but can have cycle), and has no parallel edges (cycle of two nodes). So

• at most one edge can exist for a pair of nodes
• should look simple as well

Some definitions:

Graph: A graph consists of a set of vertices and edges:

\[G=(V,E)\]

in the example above, this graph can be denoted as

\[G=(\{u,v,w,x,y,z\},\{e_1,...,e_8\})\]

Edge: An edge in a graph joints two vertices (e.g. $u,v$). This edge can be denoted either as $uv$, ${u,v}$, or you can name it $e_1$.

More definitions

• adjacent: two nodes $u$ and $v$ are adjacent if there is an edge directly connecting them. Denoted as $u \sim v$.

• neighborhood: the set of nodes that has an edge directly connecting it. Denoted as

  \[\mathcal{N}(x)=\{ v \in V | v \sim x \}\]

• degree: The number of neighbors of a vertex is called its degree, denoted

  \[d(x) = |\mathcal{N}(x)|\]

  for example, $d(w)=2$ in the above figure as there are two connections. Furthermore, we denote

  • max degree of a graph as $\Delta(G)$. In the above figure $\Delta(G)=5$
  • min degree of a graph as $\delta(G)$. In the above figure $\delta(G)=1$

Observe that in the above example

So why twice? The proof is quite intuitive

• adding each edge adds a total degree of 2 to the graph
• if there are $\vert E\vert$ edges, then total degree is $2\vert E\vert$.

Handshaking: The sum of the degrees of each vertex in a graph $G=(V,E)$ is equal to twice the number of edges.

\[\sum_{u\in V}d(v) = 2|E|\]

(this holds for non-simple graphs as well, if you treat a loop as an edge)

This also means that a graph's total degree must be even.

Isomorphism

Now, we move to studying isomorphism between graphs, which arises when two graphs have the “same form.”

Isomorphism: Two graphs $G=(V_G, E_G)$ and $H=(V_H, E_H)$ are isomorphic (“same-form”) if and only if there exists a bijective function (i.e. mapping of vertices) representing an isomorphism of $G$ to $H$:

\[f:V_G \to V_H\]

such that

\[\forall u,v \in V_G, \quad u \sim v \text{ in $G$} \iff f(u) \sim f(v) \text{ in $H$}\]

i.e. it requires adjacency between vertices is the same

Below would be an example

But below is not

because realize that the left graph has an edge connecting a vertex with (degree = 1) with (degree = 3), but the right graph only has (degree = 2) with (degree = 3).

In general:

• to prove isomorphism: find a bijection and show that the adjacency property (edge to endpoints) is preserved
  • this is generally considered a hard problem, as there is no efficient algorithm to find the bijection.
• to prove non-isomorphism: if adjacency are preserved, then there will be some invariant properties such as degrees. Therefore, if some properties are violated then they cannot be isomorphic

Types of Graphs

some common types of graphs, which can have some useful properties.

Null graph: A graph that does not have edges. So you have $G=(V, {})$. This is also often denoted as

\[L_n = \text{null graph with n nodes}\]

e.g $L_1$ is one vertex zero edge, $L_2$ is two vertex zero edge, …

Complete graph: A graph with every possible pair of vertices has an edge. We use $K_n$ to denote a complete graph with $n$ vertices.

for example:

notice that

• $K_1 = L_1$!
• for every vertex $v$, it has $\deg(v)=n-1$!

Path graph: A path graph has vertices ${v_1,…,v_n}$ and edges ${e_1,…,e_{n-1}}$ such that an edge $e_k$ joins ${v_k, v_{k+1}}$. We use $P_n$ to denote path graphs with $n$ vertices.

For example

notice that $\vert V\vert -1=\vert E\vert$.

Cycle Graph: A path graph has vertices ${v_1,…,v_n}$ and edges ${e_1,…,e_{n}}$ such that an edge $e_k$ joins ${v_k, v_{k+1}}$ where $k+1$ is “$\bmod n$”. We use $C_n$ to denote path graphs with $n$ vertices.

For example:

where notice that:

• all vertex has exactly degree 2
• and $\vert V\vert =\vert E\vert$.

Regular Graph: A graph is regular provided every vertex has the same degree

• so a $C_n$ is a regular graph of degree 2
• a $K_n$ complete graph is also regular of degree $n-1$
• a $L_n$ is also a regular of degree 0.

Properties of Graphs

Now we can talk about certain properties. First a few more definitions.

Walk: A walk in $G$ is just any sequence of vertices where each vertex is adjacent to the next vertex (i.e. you can physically walk on the graph given this sequence).

For example, given this graph

where:

• $(u,v,w,v,x)$ is a walk of length 4.
• $(v)$ is a walk of length 0.
• $(u,u,x,v,w)$ is NOT a walk because $u$ does not have a connection to $u$

Path: A path in a graph is a walk in which no vertex is repeated. We denote a path of length $n-1$ with $n$ vertices as $P_n$.

Additionally, we denote $(u,v)$-path is a path that starts at vertex $u$ and ends at vertex $v$.

Then we can define

Connected Graph: A graph $G=(V,E)$ is called a connected graph provided each pair of vertices is connected by a path (i.e. you can reach any vertex from some random vertex). Formally:

\[\forall u, v \in V,\quad \exists (u,v)\text{-path}\]

connected	disconnected

Trees

Tree: Let $T=G=(V,E)$. $G$ is a tree iff it is connected and has no cycle (acyclic). A cycle can be seen as a path in which the first and last variables are the same. A graph that is acyclic contains no such paths.

some properties of trees include:

• there is exactly one path to reach from one vertex to another (since there is no cycle)
• for a tree $\vert V\vert = \vert E\vert +1$ (which can be proven by induction)
• A graph is a tree if and only if it a minimal connected (if you take out one edge, it becomes disconnected)

Leaf: let $G=(V,E)$, then a vertex of degree 1 is called a leaf in a tree. And if you take out any of the leaf nodes, you still have a tree

Theorem: let $G=(V,E)$. $G$ is tree provided that

\[\forall u,v \in V \quad \exists!\text{u-v path}\]

Theorem: for a tree $\vert V\vert =\vert E\vert +1$

Proof: by induction.

• base case: $\vert V\vert =1$ with $\vert E\vert =0$ holds with tree of 1 vertex

• inductive hypothesis: suppose $T_k$ is a tree with $k$ vertices. Suppose the proposition holds for $T_k$.

  \[|E_{T_k}| = |V_{T_k}| - 1\]

  i.e. it has $k$ vertices with $k-1$ edges.

• inductive step: it works for a tree $T_{k+1}$, because $T_{k+1}$ must be $T_k$ plus a leaf node. So suppose we derach one leaf of $T_{k+1}$, we get a tree $T_k$. Therefore it means $T_{k+1}$ has one extra edge than $T_k$ (and one leaf node).

  \[|E_{T_{k+1}}|=k=(k+1)-1\]

  holds

Hamiltonian Path: is a path containing all vertices (recall that a path walk without repeating vertices).

• How many walks are there between $a,b$? There is an infinity of walks since there are cycles

• How many paths are there between $a,b$? There are $4\times 2= 8$. How?

  • it is equivalent to #ways to reach $a_7$ from $a$ times #ways to reach from $a_7$ to $b$.

There is no Hamiltonian path between $a$ and $b$. (complicated, in this case by enumeration)

For Example: let $K_n$ be a complete graph with $n\ge 2$. How many Hamiltonian paths are there in total, between any pair of vertices?

• notice that a complete graph is one for every pair of vertex there is an edge.
  • for $K_2$, since you can reach any from any other, there are two boxes = $2!$ ways (ab and ba)
  • for $K_3$, you have $3!$ ways (abc, acb, bac, bca, cab, cba)
  • for $K_4$, you have $4!$ ways
• so in total $n!$ Hamiltonian path for $K_n$

Eulerian Graphs

Eulerian trail: a walk in $G=(V,E)$ is called an eulerian trail provided it traverses every edge exactly once.

Eulerian tour: if an Eulerian trail start and end at the same vertex, it is called an Eulerian tour.

Eulerian graph: A graph with an Eulerian tour is called an Eulerian graph.

For example: consider the following graphs

• for graph $H$, we can
  • have an Eulerian trail fromx to y: $x-v-u-w-v-y-w-x-y$.
  • there is no Eulerian tour in $H$.
• for graph $G$, we can
  • no Eulerian tour nor Eulerian trail in $G$

How do we justify? Realize if you have even one vertex with odd degrees, then there cannot be an Eulerian tour.

• because to go out and get back, you in general must do out and in. So the degree has to be even.

Theorem: let $G$ be a connected graph. If every vertex $v\in V(G)$ has even degree, then there is an Eulerian tour that begins and ends at (every) $v$

Theorem: let $G$ be a connected graph with exactly two vertices of odd degree $u,v$. Then $G$ has a Eulerian trail that begins at $u$ and ends at $v$.

For Example: how many non-isomorphic graph with $n$ vertices are there? Given $n=4$,

• there are ${4 \choose 2}=6$ possible edges to place into a graph of 4 nodes.

• for every graph, you can choose to have the edge or not. Hence $2^6$ possible graphs (including isomorphic)

  \[\square \square \square \square \square \square\]

• for non-isomorphic graph, you will need to draw all the equivalence groups/isomorphism

• there you will find there are 11 of them/non-isomorphic graph

There is an formula for this, but in the course we pretend we don’t know, and we have to count.

Planar Graphs

Is it possible to feed every house with utility without a cable (edge) crossing other edges?

Planar Graph: A graph is a planar graph if it can be drawn in a two-dimensional space with no crossing edges. A planar graph divides the plane into areas called faces.

For Example: square graph being planar v.s. not planar.

non-planar	planar

where the planar graph no the right has “non-overlapping” faces.

Theorem: For every connected planar graph, we have:

\[v+f = e+2\]

where $v$ is the number of vertices, $e$ the number of edges, and $f$ the number of faces.